
【题目】如图,在平面直角坐标系中,直线![]() 与直线
与直线![]() 交于点
交于点![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴上,过点
轴上,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
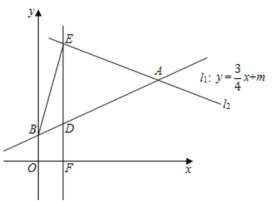
(1)求直线![]() 的解析式和
的解析式和![]() 点坐标.
点坐标.
(2)求①![]() 的面积
的面积![]() 与
与![]() 的关系式.并求出当
的关系式.并求出当![]() 的面积为
的面积为![]() 时,点
时,点![]() 坐标.在
坐标.在![]() 轴上确定点
轴上确定点![]() ,使得
,使得![]() 的面积等于
的面积等于![]() 面积,直接写出点
面积,直接写出点![]() 的坐标;
的坐标;
②若直线![]() 将
将![]() 分成面积相等的两部分,求
分成面积相等的两部分,求![]() 的值.
的值.
③若![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,使得当
上一点,使得当![]() 沿着
沿着![]() 折叠后与
折叠后与![]() 重合,请直接写出点
重合,请直接写出点![]() 和点
和点![]() 的坐标.
的坐标.
【答案】(1)点B为(0,1),直线l1:y=![]() x+1;直线l2:y=
x+1;直线l2:y=![]() x+8;(2)①点M的坐标为:(0,
x+8;(2)①点M的坐标为:(0,![]() )或(0,
)或(0,![]() );②k=
);②k=![]() ;③点Q(0,1),点P为(1,1).
;③点Q(0,1),点P为(1,1).
【解析】
(1)l1与y轴交于点B,则点B(0,m),将点A、B的坐标代入l1:y=![]() x+m并解得:m=1,故点A、B的坐标分别为:(4,4)、(0,1),即可求解;
x+m并解得:m=1,故点A、B的坐标分别为:(4,4)、(0,1),即可求解;
(2)①设点M(0,t),△BMA的面积等于△BEA面积,则点M、E所在的直线与AB平行,即可求解;
②直线y=kx-k+7=k(x-1)+7,当x=1时,y=7,即直线过点(1,7),即过点E,设直线交AB于点R,直线y=kx-k+7将△BEA分成面积相等的两部分,则点R是AB的中点,坐标为:(2,![]() ),即可求解;
),即可求解;
③如图2,AB=5,AF=5,故AB=AF,则当△PFA沿着AP折叠后与△QPA重合时,点Q与点B重合,即点Q(0,1),即可求解.
解:(1)l1与y轴交于点B,则点B(0,m),
将点A、B的坐标代入l1:y=![]() x+m并解得:m=1,
x+m并解得:m=1,
∴点A、B的坐标分别为:(4,4)、(0,1),
将点A坐标代入l2表达式并解得:k=![]() 1,
1,
∴直线l1:y=![]() x+1;直线l2:y=
x+1;直线l2:y=![]() x+8;
x+8;
(2)设点F(a,0),则点D(a,![]() a+1)、点E(a,-a+8),
a+1)、点E(a,-a+8),
△BEA的面积=![]() ×DE×xA=
×DE×xA=![]() ×(-a+8-
×(-a+8-![]() a-1)×4=
a-1)×4=![]() ,
,
解得:a=1,
故点F、D、E的坐标分别为:(1,0)、(1,![]() )、(1,7);
)、(1,7);
①设点M(0,t),△BMA的面积等于△BEA面积,则点M、E所在的直线与AB平行,
当M在AB上方时,
由E、M的坐标的直线EM的表达式为:y=![]() x+t,
x+t,
将点E的坐标代入上式并解得:t=![]() ,
,
故点M(0,![]() );
);
当M(M′)在AB下方时,
则点M′、M关于点B对称,则点M′(0,![]() ),
),
故点M的坐标为:(0,![]() )或(0,
)或(0,![]() );
);
②直线y=kx-k+7=k(x-1)+7,当x=1时,y=7,即直线过点(1,7),即过点E,
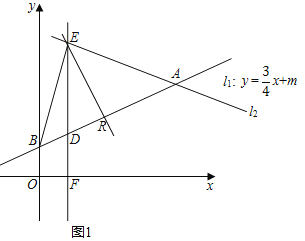
设直线交AB于点R,直线y=kx-k+7将△BEA分成面积相等的两部分,
则点R是AB的中点,坐标为:(2,![]() );
);
将点R的坐标代入y=kx-k+7,
∴![]() ,
,
解得:k=![]() ;
;
③如图2,AB=5,AF=5,故AB=AF,
则当△PFA沿着AP折叠后与△QPA重合时,点Q与点B重合,即点Q(0,1)
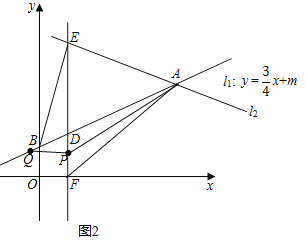
而OF=1,而PQ=PF,故PF=1,
故点P为(1,1).


科目:初中数学 来源: 题型:
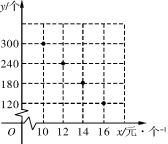
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:
(1) ![]() 与
与![]() 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润![]() (单位:元)与销售单价
(单位:元)与销售单价![]() (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F,
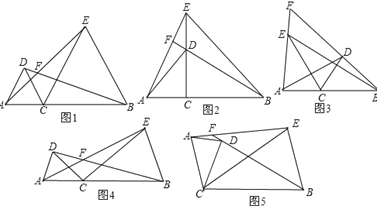
(1)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;如图3,若∠ACD=120°,则∠AFB= ;
(2)如图4,若∠ACD=α,则∠AFB= (用含α的式子表示);
(3)将图4中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),变成如图5所示的情形,若∠ACD=α,则∠AFB与α的有何数量关系?并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午![]() ,下午
,下午![]() ,每月
,每月![]() 天;
天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于![]() 件.
件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品数(件) | 生产乙产品数(件) | 所用时间 (分) |
|
|
|
|
|
|
信息三:按件计酬:每生产一件甲产品可得![]() 元,每生产一件乙产品可得
元,每生产一件乙产品可得![]() 元.
元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟;
(2)小王该月最多能得多少元,此时生产甲、乙两种产品分别多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,,
,,![]()
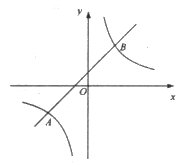
(1)求反比例函数与一次函数的函数表达式
(2)请结合图像直接写出不等式![]() 的解集;
的解集;
(3)若点P为x轴上一点,△ABP的面积为10,求点P的坐标,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )

A. ∠D=∠C B. BD=AC C. ∠CAD=∠DBC D. AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() 和
和![]() 交于点
交于点![]() .
.

(1)求证:![]() ;
;
(2)下列结论中,正确的有________个.
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() .
.
(3)请选择(2)中任一正确结论进行证明.你选的序号是 _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC、BD是四边形ABCD的对角线,若E、F、G、H分别是BD、BC、AC、AD的中点,顺次连接E、F、G、H四点,得到四边形EFGH,则下列结论不正确的是( )
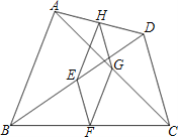
A.四边形EFGH一定是平行四边形B.当AB=CD时,四边形EFGH是菱形
C.当AC⊥BD时,四边形EFGH是矩形D.四边形EFGH可能是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com