
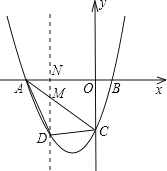
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
【答案】(1)y=![]() x2+
x2+![]() x﹣3;(2)
x﹣3;(2)![]() .
.
【解析】
试题分析:(1)已知了B点坐标,易求得OB、OC的长,进而可将B、C的坐标代入抛物线中,求出待定系数的值,即可得出抛物线的解析式.
(2)根据A、C的坐标,易求得直线AC的解析式.由于AB、OC都是定值,则△ABC的面积不变,若四边形ABCD面积最大,则△ADC的面积最大;可过D作x轴的垂线,交AC于M,x轴于N;易得△ADC的面积是DM与OA积的一半,可设出N点的坐标,分别代入直线AC和抛物线的解析式中,即可求出DM的长,进而可得出四边形ABCD的面积与N点横坐标间的函数关系式,根据所得函数的性质即可求出四边形ABCD的最大面积.
解:(1)∵B(1,0),
∴OB=1;
∵OC=3BO,
∴C(0,﹣3);(1分)
∵y=ax2+3ax+c过B(1,0)、C(0,﹣3),
∴![]() ;
;
解这个方程组,得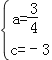 ,
,
∴抛物线的解析式为:y=![]() x2+
x2+![]() x﹣3;
x﹣3;
(2)过点D作DM∥y轴分别交线段AC和x轴于点M、N
在y=![]() x2+
x2+![]() x﹣3中,令y=0,
x﹣3中,令y=0,
得方程![]() x2+
x2+![]() x﹣3=0解这个方程,得x1=﹣4,x2=1
x﹣3=0解这个方程,得x1=﹣4,x2=1
∴A(﹣4,0)
设直线AC的解析式为y=kx+b
∴![]() ,
,
解这个方程组,得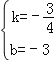 ,
,
∴AC的解析式为:y=﹣![]() x﹣3,
x﹣3,
∵S四边形ABCD=S△ABC+S△ADC
=![]() +
+![]() DM(AN+ON)
DM(AN+ON)
=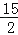 +2DM
+2DM
设D(x,![]() x2+
x2+![]() x﹣3),M(x,﹣
x﹣3),M(x,﹣![]() x﹣3),DM=﹣
x﹣3),DM=﹣![]() x﹣3﹣(
x﹣3﹣(![]() x2+
x2+![]() x﹣3)=﹣
x﹣3)=﹣![]() (x+2)2+3,
(x+2)2+3,
当x=﹣2时,DM有最大值3
此时四边形ABCD面积有最大值![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
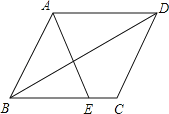
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+px+q图象的顶点M为直线y=![]() x+
x+![]() 与y=-x+m-1的交点,
与y=-x+m-1的交点,
(1)用含m的代数式来表示顶点M的坐标(直接写出答案);
(2)当x≥2时,二次函数y=x2+px+q与y=![]() x+
x+![]() 的值均随x的增大而增大,求m的取值范围
的值均随x的增大而增大,求m的取值范围
(3)若m=6,当x取值为t-1≤x≤t+3时,二次函数y最小值=2,求t的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陕西省元月份某一天的天气预报中,延安市的最低气温为﹣6℃,西安市的最低气温为2℃,这一天延安市的最低气温比西安市的最低气温低( )
A.8℃
B.﹣8℃
C.6℃
D.2℃
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com