

分析 (1)①根据题意画出图形即可;
②连接CH,先根据正方形的性质得出△DHQ是等腰直角三角形,再由SAS定理得出△HDP≌△HQC,故PH=CH,∠HPC=∠HCP,由正方形的性质即可得出结论;
(2)根据四边形ABCD是正方形,QH⊥BD可知△DHQ是等腰直角三角形,再由平移的性质得出PD=CQ.作HR⊥PC于点R,由∠AHQ=150°,可得出∠AHB及∠DAH的度数,设DP=x,则DR=HR=RQ,由锐角三角函数的定义即可得出结论
解答 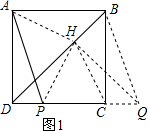 解:(1)①如图1;
解:(1)①如图1;
②AH=PH,AH⊥PH.
如图1,连接CH,
∵QH⊥BD,
∴∠QHB=∠BCQ=90°,
∴B、H、C、Q四点共圆,
∴∠DHC=∠BQC,
由正方形的性质可知∠DHC=∠AHD,
由平移性质可知∠BQC=∠APD,
∴∠AHD=∠APD,
∴A、H、P、D四点共圆,
∴∠PAH=∠PDH=45°,∠AHP=∠ADP=90°,
∴△HAP是等腰直角三角形,
∴AH=PH,AH⊥PH.
(2)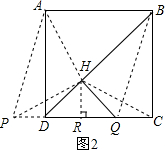
由(1)②可知∠AHP=90°,
∴∠AHP=∠ADP=90°,
∴A、H、D、P四点共圆,
又∠AHQ=150°,∠BHQ=90°,
∴∠AHB=150°-90°=60°,
由圆的性质可知∠APD=∠AHB=60°,
在Rt△APD中,∠PAD=90°-60°=30°,
∴PD=AD•tan30°=tan30°=$\frac{\sqrt{3}}{3}$.
点评 此题是四边形综合题,主要考查了正方形的性质、图形平移的性质、全等三角形的判定与性质等知识,难度适中,解决本题的关键是熟记全等三角形的性质定理和判定定理.


科目:初中数学 来源: 题型:选择题
| A. | 45° | B. | 55° | C. | 45°或55° | D. | 55°或65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
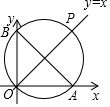 如图,平面直角坐标系中,A、B两点的坐标分别为(6,0)、(0,8),以AB为直径的圆与直线y=x交于点P,则点P的坐标是( )
如图,平面直角坐标系中,A、B两点的坐标分别为(6,0)、(0,8),以AB为直径的圆与直线y=x交于点P,则点P的坐标是( )| A. | (6.5,6.5) | B. | (7,7) | C. | (7.5,7.5) | D. | (8,8) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | mx+nx+k=(m+n)x+k | B. | x2-9=(x+3)(x-3) | ||
| C. | x2-4+3x=(x+2)(x-2)-3x | D. | (a+b)(a-b)=a2-b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com