
【题目】已知:如图,点B、C、E三点在同一条直线上, CD平分∠ACE, DB=DA,DM⊥BE于M.
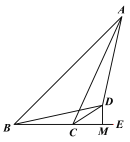
(1)求证:AC=BM+CM;
(2)若AC=2,BC=1,求CM的长.
【答案】(1)见解析;(2)CM=0.5
【解析】
(1)作DN⊥AC于N,易证Rt△DCN≌Rt△DCM,可得CN=CM,进而可以证明Rt△ADN≌Rt△BDM,可得AN=BM,即可解题;(2)利用(1)中的结论变形得出答案即可.
(1)证明:如图,作DN⊥AC于点N,
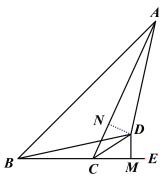
∵CD平分∠ACE,DM⊥BE,∴DN=DM,
在Rt△DCN和Rt△DCM中,
![]() ,
,
∴Rt△DCN≌Rt△DCM(HL),
∴CN=CM,
在Rt△ADN和Rt△BDM中,
![]() ,
,
∴Rt△ADN≌Rt△BDM(HL),∴AN=BM,
∵AC=AN+CN,∴AC=BM+CM;
(2)∵AN=AC-CN, BM=BC+CM,∴AC-CN=BC+CM,
∴AC-CM=BC+CM,∴2CM=AC-BC,
∵AC=2,BC=1,∴CM=0.5.


科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为8,AD是BC边上的中线,点E是AC边上的一点,AE=2,若点M是线段AD上的一个动点,则ME+MC的最小值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行20分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是___________海里.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
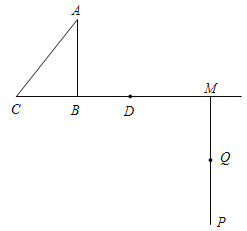
【题目】如图,在Rt△ABC中,AB=4,BC=3,点D从B点出发,沿射线CB方向以每秒3个单位长度的速度运动,射线MP⊥射线CB,且BM=10,点Q从M点出发,沿射线MQ方向以每秒a个单位长度的速度运动,已知D、Q两点同时出发,运动时间为t秒.
(1)当t=2时,△DMQ是等腰三角形,求a的值.
(2)求t为何值时,△DCA为等腰三角形.
(3)是否存在a,使得△DMQ与△ABC全等,若存在,请直接写出a的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠ABC=90°,△ABC是等腰三角形,点D为斜边AC的中点,连接DB,过点A作∠BAC的平分线,分别与DB,BC相交于点E,F.
(1)求证:BE=BF;
(2)如图2,连接CE,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的数学活动课上,小明和小刚制作了一个正三楼锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下每人投掷三棱锥两次,并记录底面的数字,如果两次所掷数字的和为单数,那么算小明赢,如果两欢所掷数字的和为偶数,那么算小明赢;
(1)请用列表或者面树状围的方法表示上述游戏中的所有可能结果.
(2)请分别隶出小明和小刚能赢的概率,并判新游戏的公平性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠C=∠EDF=60°,AB=1,现将∠EDF绕点D任意旋转,分别交边AB、BC于点E、F(不与菱形的顶点重合),连接EF,则△BEF的周长最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请利用直尺完成下列问题
(1)如图(1)示,利用网格画图:

①在BC上找一点P,使得P到AB和AC的距离相等;
②在射线AP上找一点Q,使QB=QC.
(2)如图(2)示,点A,B,C都在方格纸的格点上.请你再找一个格点D,使点A,B,C,D组成一个轴对称图形,请在图中标出满足条件的所有点D的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com