
【题目】如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的![]() 时,则
时,则![]() 为( )
为( )
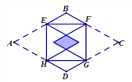
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
【答案】C
【解析】分析:设重叠的菱形边长为x,BE=BF=y,由矩形和菱形的对称性以及折叠的性质得:四边形AHME、四边形BENF是菱形,得出EN=BE=y,EM=x+y,由相似的性质得出AB=4MN=4x,求出AE=AB-BE=4x-y,得出方程4x-y=x+y,得出x=![]() y,AE=
y,AE=![]() y,即可得出结论.
y,即可得出结论.
详解:如图:
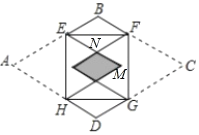
设重叠的菱形边长为x,BE=BF=y,
由矩形和菱形的对称性以及折叠的性质得:四边形AHME、四边形BENF是菱形,
∴AE=EM,EN=BE=y,EM=x+y,
∵当重叠部分为菱形且面积是菱形ABCD面积的![]() ,且两个菱形相似,
,且两个菱形相似,
∴AB=4MN=4x,
∴AE=ABBE=4xy,
∴4xy=x+y,
解得:x=![]() y,
y,
∴AE=![]() y,
y,
∴![]() =
=![]() =
=![]() ;
;
故选:C.


科目:初中数学 来源: 题型:
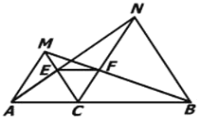
【题目】已知:如图,点C为线段AB上一点,△ACM, △CBN都是等边三角形,AM=AC=CM,BC=CN=BN,∠ACM=∠BCN=60°,AN交MC于点E,BM交CN于点F.
(1)求证:AN=BM;
(2)求证:判断△CEF形状
查看答案和解析>>
科目:初中数学 来源: 题型:
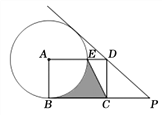
【题目】如图,已知四边形ABCD是矩形,点P在BC边的延长线上,且PD=BC,⊙A经过点B,与AD边交于点E,连接CE .
(1)求证:直线PD是⊙A的切线;
(2)若PC=2![]() ,sin∠P=
,sin∠P=![]() ,求图中阴影部份的面积(结果保留无理数).
,求图中阴影部份的面积(结果保留无理数).
查看答案和解析>>
科目:初中数学 来源: 题型:
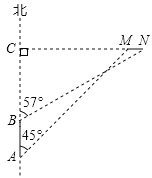
【题目】钓鱼岛自古就是中国的领土,中国有关部门已北对钓鱼岛及其附属岛屿开展常态化监视巡航![]() 一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛
一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛![]() 设N、M为该岛的东西两端点
设N、M为该岛的东西两端点![]() 最近距离为15海里
最近距离为15海里![]() 即
即![]() 海里
海里![]() ,在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东
,在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东![]() 方向
方向![]() 其中N、M、C在同一条直线上
其中N、M、C在同一条直线上![]() ,求钓鱼岛东西两端点MN之间的距离
,求钓鱼岛东西两端点MN之间的距离![]() 精确到
精确到![]() 海里,参考数据:
海里,参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
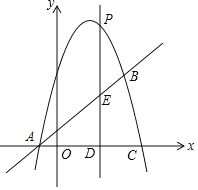
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P是抛物线上的一个动点
点P是抛物线上的一个动点![]() 不与点A、点B重合
不与点A、点B重合![]() ,过点P作直线
,过点P作直线![]() 轴于点D,交直线AB于点E.
轴于点D,交直线AB于点E.
![]() 当
当![]() 时,求P点坐标;
时,求P点坐标;
![]() 是否存在点P使
是否存在点P使![]() 为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
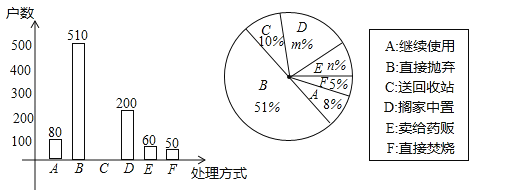
①m= ,n= ;
②补全条形统计图;
③根据调査数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某港口在某天从0时到12时的水位情况变化曲线.

(1)在这一问题中,自变量是什么?
(2)大约在什么时间水位最深,最深是多少?
(3)大约在什么时间段水位是随着时间推移不断上涨的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,分别给出以下条件:①AB∥CD;②AB=CD;③AD∥BC;④AD=BC;⑤∠A=∠C.则下列条件组合中,不能判定四边形ABCD为平行四边形的是( )

A. ①④B. ①③C. ①②D. ①⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com