
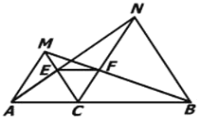
【题目】已知:如图,点C为线段AB上一点,△ACM, △CBN都是等边三角形,AM=AC=CM,BC=CN=BN,∠ACM=∠BCN=60°,AN交MC于点E,BM交CN于点F.
(1)求证:AN=BM;
(2)求证:判断△CEF形状
【答案】(1)证明见解析;(2)△CEF是等边三角形,理由见解析.
【解析】
(1)由等边三角形可得其对应线段相等,对应角相等,进而可由SAS得到△ACN≌△MCB,结论得证;
(2)由(1)中的全等可得∠CAN=∠CMB,进而得出∠MCF=∠ACE,由ASA得出△CAE≌△CMF,即CE=CF,又ECF=60°,所以△CEF为等边三角形.
(1)∵△ACM,△CBN是等边三角形,
∴AC=MC,BC=NC,∠ACM=∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,即∠ACN=∠MCB,
在△ACN和△MCB中,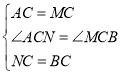 ,
,
∴△ACN≌△MCB(SAS),
∴AN=BM;
(2)△CEF是等边三角形,
理由:∵△CAN≌△CMB,
∴∠CAN=∠CMB,
又∵∠MCF=180°-∠ACM-∠NCB=180°-60°-60°=60°,
∴∠MCF=∠ACE,
在△CAE和△CMF中,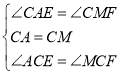 ,
,
∴△CAE≌△CMF(ASA),
∴CE=CF,
∴△CEF为等腰三角形,
又∵∠ECF=60°,
∴△CEF为等边三角形.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具厂生产一种餐桌和椅子,餐桌每张定价为![]() 元,椅子每把定价为
元,椅子每把定价为![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:每买一张餐桌就赠送一把椅子;
方案二:餐桌和椅子都按定价的![]() 付款.
付款.
某餐厅计划添置![]() 张餐桌和
张餐桌和![]() 把椅子.
把椅子.
(1)若![]() ,请用含
,请用含![]() 的代数式分别把两种方案的费用表示出来.
的代数式分别把两种方案的费用表示出来.
(2)已知![]() ,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地发生地震,学校师生积极捐款,已知第一天捐款4800元,第二天捐款6000元,第二天捐款人数比第一天捐款人数多50人,且两天人均捐款数相等。
(1)求第二天参加捐款的人数是多少?
(2)第三天又有100人捐款,第三天人均捐款数与前两天相同,求第三天捐款数额
查看答案和解析>>
科目:初中数学 来源: 题型:
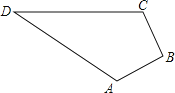
【题目】如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
(1)土地的面积是多少?
(2)蔬菜单位面积产量为20㎏,则这块地产蔬菜多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(阅读材料)
在数轴上,通常用“两数的差”来表示“数轴上两点的距离”如图1中三条线段的
长度可表示为:![]() ,
,![]() 结论:数轴上任意两点
结论:数轴上任意两点
表示的数为分别![]() ,则这两个点间的距离为
,则这两个点间的距离为![]() (即:用较大的数去减较小的数)
(即:用较大的数去减较小的数)
![]()
(理解运用)
根据阅读材料完成下列各题:
(1)如图2, ![]() 分别表示数
分别表示数![]() ,求线段
,求线段![]() 的长;
的长;
![]()
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 对应的数值.
对应的数值.
(3)![]() 两点分别从
两点分别从![]() 同时出发以3个单位、2个单位长度的速度沿数轴向右运动,求当点
同时出发以3个单位、2个单位长度的速度沿数轴向右运动,求当点![]() 重合时,它们运动的时间;
重合时,它们运动的时间;
(4)在(3)的条件下,求当![]() 时,它们运动的时间.
时,它们运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的![]() 时,则
时,则![]() 为( )
为( )
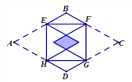
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com