
【题目】如图是某港口在某天从0时到12时的水位情况变化曲线.

(1)在这一问题中,自变量是什么?
(2)大约在什么时间水位最深,最深是多少?
(3)大约在什么时间段水位是随着时间推移不断上涨的?
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
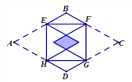
【题目】如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的![]() 时,则
时,则![]() 为( )
为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果一个点的纵坐标等于横坐标的2倍,那么这个点叫做倍点.例如:点(1,2)是倍点。
(1)已知第一象限内的点A到x轴的距离是1,若点A是倍点,则点A的坐标为________
(2)求反比例函数![]() 图像上的所有倍点;
图像上的所有倍点;
(3)请分析一次函数![]() (
(![]() 为常数)图像上倍点的情况.
为常数)图像上倍点的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
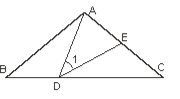
【题目】如图,⊿ABC中,AB=AC,∠BAC=![]() ,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
(1)若∠BAD=![]() ,求∠EDC的度数;
,求∠EDC的度数;
(2)当DC=AC时,求证:⊿ABD≌⊿DCE ;
(3)当∠BAD的度数是多少时,⊿ADE能成为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
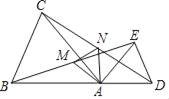
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
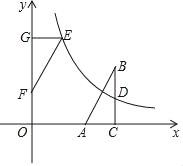
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
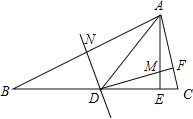
【题目】如图,在△ABC中,AE⊥BC于点E,∠B=22.5°,AB的垂直平分线DN交BC于点D,交AB于点N,DF⊥AC于点F,交AE于点M.求证:
(1)AE=DE;
(2)EM=EC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com