
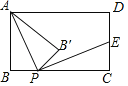
【题目】如图,矩形ABCD中,AB=2,BC=4,点P是BC边上的一个动点(点P不与点B,C重合),现将△ABP沿直线AP折叠,使点B落到点B′处;作∠B′PC的角平分线交CD于点E.设BP=x,CE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.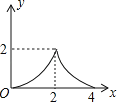 B.
B.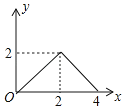
C.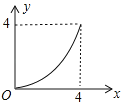 D.
D.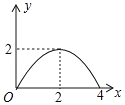
科目:初中数学 来源: 题型:
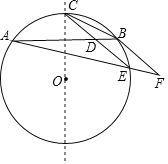
【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1:![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的部分图象如图,则下列说法错误的是( )
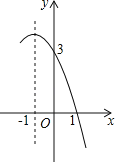
A. 对称轴是直线x=﹣1
B. abc<0
C. b2﹣4ac>0
D. 方程ax2+bx+c=0的根是x1=﹣3和x2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
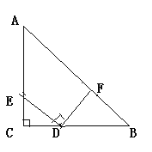
【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
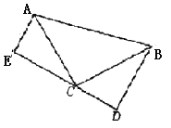
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
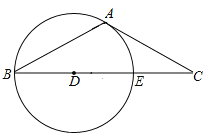
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上,⊙D经过点A和点B且与BC边相交于点E.
(1)求证:AC是⊙D的切线;
(2)若CE=2![]() ,求⊙D的半径.
,求⊙D的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
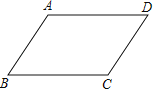
【题目】如图,在平行四边形ABCD中,AD>AB.
(1)作∠BAD的平分线交BC于点E,在AD边上截取AF=AB,连接EF(要求:尺规作图,保留作图痕迹,不写作法);
(2)判断四边形ABEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架无人机在距离地面高度为13.3米的点A处,测得地面点M的俯角为53°,这架无人机沿仰角为35°的方向飞行了55米到达点B,恰好在地面点N的正上方,M、N在同一水平线上求出M、N两点之间的距离.(结果精确到1米)
(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,其自变量的取值范围是x>-2,当x=2时,y1=-2;当x=6时,y1=-5.
,其自变量的取值范围是x>-2,当x=2时,y1=-2;当x=6时,y1=-5.
(1)根据给定的条件,求出a、b的值和y1的函数解析式;
(2)根据你所求的函数解析式,选取适当的自变量x完成下表,并在下面的平面直角坐标系中描点并画出函数的大致图象.
x | … | 6 | … | |||||||
y | … | -5 | … |
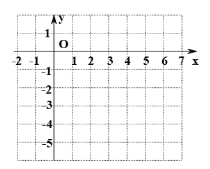
(3)请画出y2=x-4的图象,并结合图象直接写出:当y1>y2时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市举办的以“校园文明”为主题的中小学生手抄报比赛中,各学校认真组织初赛并按比例筛选出较好的作品参加全市决赛,所有参加市级决赛的作品均获奖,奖项分为一等奖.二等奖、三等奖和优秀奖.现从参加决赛的作品中随机抽取部分作品并将获奖结果绘制成如下两幅统计图请你根据图中所给信息解答下列问题:

(1)一等奖所占的百分比是多少?三等奖的人数是多少?
(2)求三等奖所对应的扇形圆心角的度数;
(3)若参加决赛的作品有3000份,估计获得一等奖和二等奖的总人数有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com