
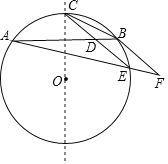
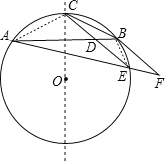
【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1:![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
【答案】①证明见解析;②△BCD的面积为:2.
【解析】
试题分析:①连接AC,BE,由等腰三角形的性质和三角形的外角性质得出∠F=![]() ∠AEB,由圆周角定理得出∠AEC=∠BEC,证出∠AEC=∠F,即可得出结论;
∠AEB,由圆周角定理得出∠AEC=∠BEC,证出∠AEC=∠F,即可得出结论;
②证明△ADE∽△CBE,得出![]() ,证明△CBE∽△CDB,得出
,证明△CBE∽△CDB,得出![]() ,求出CB=2
,求出CB=2![]() ,得出AD=6,AB=8,由垂径定理得出OC⊥AB,AG=BG=
,得出AD=6,AB=8,由垂径定理得出OC⊥AB,AG=BG=![]() AB=4,由勾股定理求出CG=
AB=4,由勾股定理求出CG=![]() =2,即可得出△BCD的面积.
=2,即可得出△BCD的面积.
试题解析:①证明:连接AC,BE,作直线OC,如图所示:
∵BE=EF,
∴∠F=∠EBF;
∵∠AEB=∠EBF+∠F,
∴∠F=![]() ∠AEB,
∠AEB,
∵C是![]() 的中点,∴
的中点,∴![]() ,
,
∴∠AEC=∠BEC,
∵∠AEB=∠AEC+∠BEC,
∴∠AEC=![]() ∠AEB,
∠AEB,
∴∠AEC=∠F,
∴CE∥BF;
②解:∵∠DAE=∠DCB,∠AED=∠CEB,
∴△ADE∽△CBE,
∴![]() ,即
,即![]() ,
,
∵∠CBD=∠CEB,∠BCD=∠ECB,
∴△CBE∽△CDB,
∴![]() ,即
,即![]() ,
,
∴CB=2![]() ,
,
∴AD=6,
∴AB=8,
∵点C为劣弧AB的中点,
∴OC⊥AB,AG=BG=![]() AB=4,
AB=4,
∴CG=![]() =2,
=2,
∴△BCD的面积=![]() BDCG=
BDCG=![]() ×2×2=2.
×2×2=2.


科目:初中数学 来源: 题型:
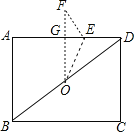
【题目】如图,在矩形ABCD中,AB=6,BC=8,点O为对角线BD的中点,点E为边AD上一点,连接OE,将△DOE沿OE翻折得到△OEF,若OF⊥AD于点G,则OE=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
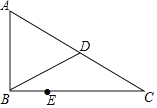
【题目】在Rt△ABC中,∠ABC=90°,∠C=30°,AC=8,BD为边AC上的中线,点E在边BC上,且BE:BC=3:8,点P在Rt△ABC的边上运动,当PD:AB=1:2时,EP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
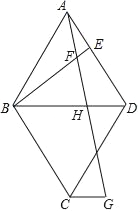
【题目】如图,菱形ABCD中,∠BAD=60°,点E在边AD上,连接BE,在BE上取点F,连接AF并延长交BD于H,且∠AFE=60°,过C作CG∥BD,直线CG、AF交于G.
(1)求证:∠FAE=∠EBA;
(2)求证:AH=BE;
(3)若AE=3,BH=5,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
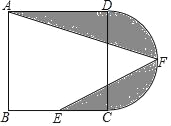
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了![]() 名学生(每名学生必选且只能选择这五项活动中的一种).
名学生(每名学生必选且只能选择这五项活动中的一种).
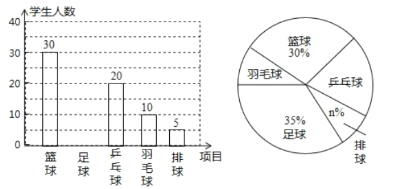
根据以上统计图提供的信息,请解答下列问题:
(1)![]() ,
,![]() .
.
(2)补全上图中的条形统计图.
(3)若全校共有![]() 名学生,请求出该校约有多少名学生喜爱打乒乓球.
名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的![]() 名学生中,有小薇、小燕、小红、小梅等
名学生中,有小薇、小燕、小红、小梅等![]() 名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这
名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这![]() 名女生中,选取
名女生中,选取![]() 名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母
名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母![]() 、
、![]() 、
、![]() 、
、![]() 代表)
代表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,BC=4,点P是BC边上的一个动点(点P不与点B,C重合),现将△ABP沿直线AP折叠,使点B落到点B′处;作∠B′PC的角平分线交CD于点E.设BP=x,CE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
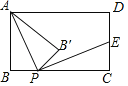
A.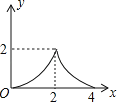 B.
B.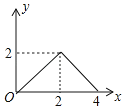
C.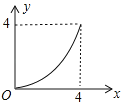 D.
D.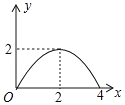
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com