
ЎҫМвДҝЎҝОТКР¶«ЖВКөСйЦРС§ЧјұёҝӘХ№Ў°Сф№вМеУэ»о¶ҜЎұЈ¬ҫц¶ЁҝӘЙиЧгЗтЎўАәЗтЎўЖ№ЕТЗтЎўУрГ«ЗтЎўЕЕЗтөИЗтАа»о¶ҜЈ¬ОӘБЛБЛҪвС§Йъ¶ФХвОеПо»о¶ҜөДПІ°®ЗйҝцЈ¬Лж»ъөчІйБЛ![]() ГыС§ЙъЈЁГҝГыС§ЙъұШСЎЗТЦ»ДЬСЎФсХвОеПо»о¶ҜЦРөДТ»ЦЦЈ©Ј®
ГыС§ЙъЈЁГҝГыС§ЙъұШСЎЗТЦ»ДЬСЎФсХвОеПо»о¶ҜЦРөДТ»ЦЦЈ©Ј®
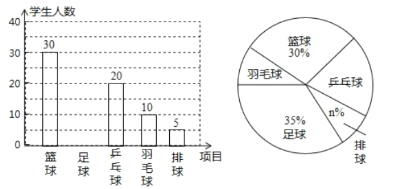
ёщҫЭТФЙПНіјЖНјМṩөДРЕПўЈ¬ЗлҪвҙрПВБРОКМвЈә
ЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј®
Ј®
ЈЁ2Ј©І№И«ЙПНјЦРөДМхРОНіјЖНјЈ®
ЈЁ3Ј©ИфИ«РЈ№ІУР![]() ГыС§ЙъЈ¬ЗлЗуіцёГРЈФјУР¶аЙЩГыС§ЙъПІ°®ҙтЖ№ЕТЗтЈ®
ГыС§ЙъЈ¬ЗлЗуіцёГРЈФјУР¶аЙЩГыС§ЙъПІ°®ҙтЖ№ЕТЗтЈ®
ЈЁ4Ј©ФЪійІйөД![]() ГыС§ЙъЦРЈ¬УРРЎЮұЎўРЎСаЎўРЎәмЎўРЎГ·өИ
ГыС§ЙъЦРЈ¬УРРЎЮұЎўРЎСаЎўРЎәмЎўРЎГ·өИ![]() ГыС§ЙъПІ»¶УрГ«Зт»о¶ҜЈ¬С§РЈҙтЛгҙУРЎЮұЎўРЎСаЎўРЎәмЎўРЎГ·Хв
ГыС§ЙъПІ»¶УрГ«Зт»о¶ҜЈ¬С§РЈҙтЛгҙУРЎЮұЎўРЎСаЎўРЎәмЎўРЎГ·Хв![]() ГыЕ®ЙъЦРЈ¬СЎИЎ
ГыЕ®ЙъЦРЈ¬СЎИЎ![]() ГыІОјУИ«КРЦРС§ЙъЕ®ЧУУрГ«ЗтұИИьЈ¬ЗлУГБРұн·Ё»т»ӯКчЧҙНј·ЁЈ¬ЗуН¬КұСЎЦРРЎәмЎўРЎСаөДёЕВКЈ®ЈЁҪвҙр№эіМЦРЈ¬ҝЙҪ«РЎЮұЎўРЎСаЎўРЎәмЎўРЎГ··ЦұрУГЧЦДё
ГыІОјУИ«КРЦРС§ЙъЕ®ЧУУрГ«ЗтұИИьЈ¬ЗлУГБРұн·Ё»т»ӯКчЧҙНј·ЁЈ¬ЗуН¬КұСЎЦРРЎәмЎўРЎСаөДёЕВКЈ®ЈЁҪвҙр№эіМЦРЈ¬ҝЙҪ«РЎЮұЎўРЎСаЎўРЎәмЎўРЎГ··ЦұрУГЧЦДё![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() ҙъұнЈ©
ҙъұнЈ©
Ўҫҙр°ёЎҝЈЁ1Ј©100Ј»5Ј»ЈЁ2Ј©ЧгЗт35ИЛЈ¬НјјыҪвОцЈ»ЈЁ3Ј©400ИЛЈ»ЈЁ4Ј©![]() .
.
ЎҫҪвОцЎҝ
ЈЁ1Ј©АәЗт30ИЛХј30%Ј¬ҝЙөГЧЬИЛКэЈ¬УЙҙЛҝЙТФјЖЛгіцnЈ»
ЈЁ2Ј©ЗуіцЧгЗтИЛКэ=100-30-20-10-5=35ИЛЈ¬јҙҝЙҪвҫцОКМвЈ»
ЈЁ3Ј©УГСщұҫ№АјЖЧЬМеөДЛјПлјҙҝЙҪвҫцОКМвЈ®
ЈЁ4Ј©»ӯіцКчЧҙНјјҙҝЙҪвҫцОКМвЈ®
ҪвЈәЈЁ1Ј©УЙМвТвm=30ЎВ30%=100Ј¬ЕЕЗтХј![]() =5%
=5%
Ўаn=5Ј¬
№Кҙр°ёОӘ100Ј¬5Ј®
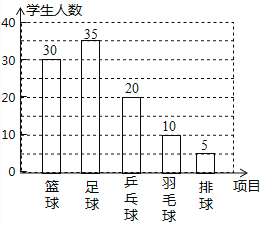
ЈЁ2Ј©ЧгЗт=100-30-20-10-5=35ИЛЈ¬
МхРОНјИзНјЛщКҫЈ¬
ЈЁ3Ј©ИфИ«РЈ№ІУР2000ГыС§ЙъЈ¬ёГРЈФјУР2000ЎБ![]() =400ГыС§ЙъПІ°®ҙтЖ№ЕТЗтЈ®
=400ГыС§ЙъПІ°®ҙтЖ№ЕТЗтЈ®
ЈЁ4Ј©»ӯКчЧҙНјөГЈә
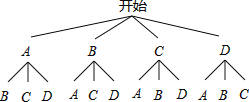
ЎЯТ»№ІУР12ЦЦҝЙДЬіцПЦөДҪб№ыЈ¬ЛьГЗ¶јКЗөИҝЙДЬөДЈ¬·ыәПМхјюөДУРБҪЦЦЈ¬
ЎаPЈЁBЎўCБҪИЛҪшРРұИИьЈ©=![]() =
=![]() Ј®
Ј®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»БҫВэіөәНТ»БҫҝміөСШПаН¬өДВ·ПЯҙУAөШөҪBөШЈ¬ЛщРРК»өДВ·іМУлКұјдөДәҜКэНјРОИзНјЛщКҫЈ¬ПВБРЛө·ЁХэИ·өДУРЈЁ Ј©
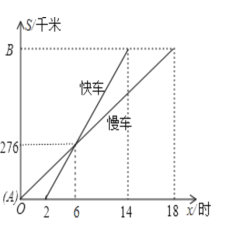
ўЩҝміөЧ·ЙПВэіөРи6РЎКұЈ»ўЪВэіөұИҝміөФзіц·ў2РЎКұЈ»ўЫҝміөЛЩ¶ИОӘ46km/hЈ»ўЬВэіөЛЩ¶ИОӘ46km/hЈ» ўЭAЎўBБҪөШПаҫа828kmЈ»ўЮҝміөҙУAөШіц·ўөҪBөШУГБЛ14РЎКұ
A. 2ёцB. 3ёцC. 4ёцD. 5ёц
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ЕЧОпПЯy=ax2+4x+cЈЁaЎЩ0Ј©ҫӯ№эөгAЈЁ3Ј¬©Ғ4Ј©әНBЈЁ0Ј¬2Ј©Ј®
ЈЁ1Ј©ЗуЕЧОпПЯөДұнҙпКҪәН¶ҘөгЧшұкЈ»
ЈЁ2Ј©Ҫ«ЕЧОпПЯФЪAЎўBЦ®јдөДІҝ·ЦјЗОӘНјПуMЈЁә¬AЎўBБҪөгЈ©Ј®Ҫ«НјПуMСШЦұПЯx=3·ӯХЫЈ¬өГөҪНјПуNЈ®Иф№эөгCЈЁ9Ј¬4Ј©өДЦұПЯy=kx+bУлНјПуMЎўНјПуN¶јПаҪ»Ј¬ЗТЦ»УРБҪёцҪ»өгЈ¬ЗуbөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
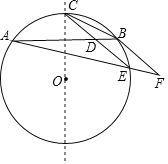
ЎҫМвДҝЎҝИзНјКҫABОӘЎСOөДТ»МхПТЈ¬өгCОӘБУ»ЎABөДЦРөгЈ¬EОӘУЕ»ЎABЙПТ»өгЈ¬өгFФЪAEөДСУіӨПЯЙПЈ¬ЗТBE=EFЈ¬ПЯ¶ОCEҪ»ПТABУЪөгDЈ®
ўЩЗуЦӨЈәCEЎОBFЈ»
ўЪИфBD=2Ј¬ЗТEAЈәEBЈәEC=3Јә1Јә![]() Ј¬ЗуЎчBCDөДГж»эЈЁЧўЈәёщҫЭФІөД¶ФіЖРФҝЙЦӘOCЎНABЈ©Ј®
Ј¬ЗуЎчBCDөДГж»эЈЁЧўЈәёщҫЭФІөД¶ФіЖРФҝЙЦӘOCЎНABЈ©Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ТСЦӘөгMЈ¬NөДЧшұк·ЦұрОӘЈЁ©Ғ1Ј¬2Ј©Ј¬ЈЁ2Ј¬1Ј©Ј¬ИфЕЧОпПЯy=ax2©Ғx+2ЈЁaЎЩ0Ј©УлПЯ¶ОMNУРБҪёцІ»Н¬өДҪ»өгЈ¬ФтaөДИЎЦө·¶О§КЗЈЁЎЎЎЎЈ©
A. aЎЬ©Ғ1»т![]() ЎЬaЈј
ЎЬaЈј![]() B.
B. ![]() ЎЬaЈј
ЎЬaЈј![]()
C. aЎЬ![]() »тaЈҫ
»тaЈҫ![]() D. aЎЬ©Ғ1»тaЎЭ
D. aЎЬ©Ғ1»тaЎЭ![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЕЧОпПЯ![]() Ул
Ул![]() ЦбҪ»УЪөг
ЦбҪ»УЪөг![]() Ј¬
Ј¬![]() Ј¬УлЦұПЯ
Ј¬УлЦұПЯ![]() Ҫ»УЪөг
Ҫ»УЪөг![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() Ул
Ул![]() ЦбҪ»УЪөг
ЦбҪ»УЪөг![]() Ј®
Ј®
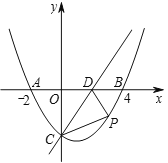
(1)ЗуёГЕЧОпПЯөДҪвОцКҪЈ®
(2)өг![]() КЗЕЧОпПЯЙПөЪЛДПуПЮЙПөДТ»ёц¶ҜөгЈ¬Б¬ҪУ
КЗЕЧОпПЯЙПөЪЛДПуПЮЙПөДТ»ёц¶ҜөгЈ¬Б¬ҪУ![]() Ј¬
Ј¬![]() Ј¬өұ
Ј¬өұ![]() өДГж»эЧоҙуКұЈ¬Зуөг
өДГж»эЧоҙуКұЈ¬Зуөг![]() өДЧшұкЈ®
өДЧшұкЈ®
(3)Ҫ«ЕЧОпПЯөД¶ФіЖЦбПтЧуЖҪТЖ3ёціӨ¶ИөҘО»өГөҪЦұПЯ![]() Ј¬өг
Ј¬өг![]() КЗЦұПЯ
КЗЦұПЯ![]() ЙПТ»өгЈ¬Б¬ҪУ
ЙПТ»өгЈ¬Б¬ҪУ![]() Ј¬
Ј¬![]() Ј¬ИфЦұПЯ
Ј¬ИфЦұПЯ![]() ЙПҙжФЪК№
ЙПҙжФЪК№![]() ЧоҙуөДөг
ЧоҙуөДөг![]() Ј¬ЗлЦұҪУРҙіцВъЧгМхјюөДөг
Ј¬ЗлЦұҪУРҙіцВъЧгМхјюөДөг![]() өДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
өДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝОвҫ©Н¬С§ёщҫЭС§П°әҜКэөДҫӯСйЈ¬¶ФТ»ёцРВәҜКэyЈҪ![]() өДНјПуәНРФЦКҪшРРБЛИзПВМҪҫҝЈ¬Зл°пЛы°СМҪҫҝ№эіМІ№ідНкХы
өДНјПуәНРФЦКҪшРРБЛИзПВМҪҫҝЈ¬Зл°пЛы°СМҪҫҝ№эіМІ№ідНкХы
ЈЁ1Ј©ёГәҜКэөДЧФұдБҝxөДИЎЦө·¶О§КЗЎЎ ЎЎЈ®
ЈЁ2Ј©БРұнЈә
x | Ўӯ | ©Ғ2 | ©Ғ1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | Ўӯ |
y | Ўӯ |
| m | ©Ғ1 |
| ©Ғ5 | n | ©Ғ1 |
|
| Ўӯ |
ұнЦРmЈҪЎЎ ЎЎЈ¬nЈҪЎЎ ЎЎЈ®
ЈЁ3Ј©ГиөгЎўБ¬ПЯ
ФЪПВГжөДёсөгНјЦРЈ¬ҪЁБўККөұөДЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ГиіцЙПұнЦРёч¶Ф¶ФУҰЦөОӘЧшұкөДөгЈЁЖдЦРxОӘәбЧшұкЈ¬yОӘЧЭЧшұкЈ©Ј¬ІўёщҫЭГиіцөДөг»ӯіцёГКэөДНјПуЈә
ЈЁ4Ј©№ЫІмЛщ»ӯіцөДәҜКэНјПуЈ¬РҙіцёГәҜКэөДБҪМхРФЦКЈә
ўЩЎЎ ЎЎЈ»
ўЪЎЎ ЎЎЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶юҙОәҜКэyЈҪax2+bx+cөДІҝ·ЦНјПуИзНјЈ¬ФтПВБРЛө·ЁҙнОуөДКЗЈЁЎЎЎЎЈ©
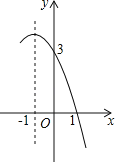
A. ¶ФіЖЦбКЗЦұПЯxЈҪ©Ғ1
B. abcЈј0
C. b2©Ғ4acЈҫ0
D. ·ҪіМax2+bx+cЈҪ0өДёщКЗx1ЈҪ©Ғ3әНx2ЈҪ1
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Т»јЬОЮИЛ»ъФЪҫаАлөШГжёЯ¶ИОӘ13.3ГЧөДөгAҙҰЈ¬ІвөГөШГжөгMөДё©ҪЗОӘ53ЎгЈ¬ХвјЬОЮИЛ»ъСШСцҪЗОӘ35ЎгөД·ҪПт·ЙРРБЛ55ГЧөҪҙпөгBЈ¬ЗЎәГФЪөШГжөгNөДХэЙП·ҪЈ¬MЎўNФЪН¬Т»Л®ЖҪПЯЙПЗуіцMЎўNБҪөгЦ®јдөДҫаАлЈ®ЈЁҪб№ыҫ«И·өҪ1ГЧЈ©
ЈЁІОҝјКэҫЭЈәsin53ЎгЎЦ0.80Ј¬cos53ЎгЎЦ0.60Ј¬tan53ЎгЎЦ1.33Ј¬sin35ЎгЎЦ0.57Ј¬cos35ЎгЎЦ0.82Ј¬tan35ЎгЎЦ0.70Ј®Ј©

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com