
分析 (1)根据幂的乘方变形,代入计算即可;
(2)先根据同底数幂乘法变形,再根据幂的乘方变形,最后代入计算可得;
(3)先根据同底数幂除法变形,再根据幂的乘方变形,最后代入计算可得.
解答 解:当10a=5,10b=6时,
(1)102a+103b=(10a)2+(10b)3
=52+63
=241;
(2)102a+3b=102a×103b
=(10a)2×(10b)3
=52×63
=5400;
(3)102a-3b=102a÷103b
=(10a)2÷(10b)3
=52÷63
=$\frac{25}{216}$.
点评 本题主要考查同底数幂乘除法、幂的乘方运算能力,恰当地选择运算法则是解题关键,属中档题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$$>\frac{a+b}{a+b+c}$ | B. | $\frac{a}{b}$$<\frac{a+b}{a+b+c}$ | C. | $\frac{a}{b}$=$\frac{a+b}{a+b+c}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
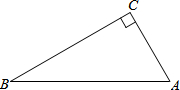 如图,在△ABC中,∠C=90°,∠A>∠B.
如图,在△ABC中,∠C=90°,∠A>∠B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com