
 如图(1)∠A与∠AEF是同旁内角;(2)∠BED与∠CFG是同位角;(3)∠AFE与∠BEF是内错角;(4)∠A与∠CFE是同位角,以上说法中,正确的是( )
如图(1)∠A与∠AEF是同旁内角;(2)∠BED与∠CFG是同位角;(3)∠AFE与∠BEF是内错角;(4)∠A与∠CFE是同位角,以上说法中,正确的是( )| A. | (1)(2) | B. | (2)(3) | C. | (1)(3)(4) | D. | (1)(2)(3)(4) |
分析 利用同位角以及内错角和同旁内角的定义:(1)同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.(2)内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.(3)同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,分别判断得出即可.
解答 解:(1)∠A与∠AEF是同旁内角,正确;
(2)∠BED与∠CFG是同位角,错误;
(3)∠AFE与∠BEF是内错角,正确;
(4)∠A与∠CFE是同位角,正确.
故选:C.
点评 此题主要考查了同位角以及内错角和同旁内角的定义,注意三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=3 | B. | 众数是7 | C. | 中位数是3 | D. | 极差是7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
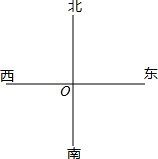 轮船在点O测得岛A在北偏东60°,距离为4千米,又测得测得岛B在点O北偏西30°,距离为3千米.①用1厘米代表1千米,画出A、B的位置.②量出图上线段AB的长度.
轮船在点O测得岛A在北偏东60°,距离为4千米,又测得测得岛B在点O北偏西30°,距离为3千米.①用1厘米代表1千米,画出A、B的位置.②量出图上线段AB的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)【阅读理解】
(1)【阅读理解】查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com