
 如图,在?ABCD中,点E是边BA延长线上的一点,CE交AD于点F.下列各式中,错误的是( )
如图,在?ABCD中,点E是边BA延长线上的一点,CE交AD于点F.下列各式中,错误的是( )| A. | $\frac{AE}{AB}=\frac{FE}{FC}$ | B. | $\frac{AE}{AB}=\frac{AF}{DF}$ | C. | $\frac{AE}{AB}=\frac{AF}{BC}$ | D. | $\frac{AE}{BE}=\frac{AF}{BC}$ |
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
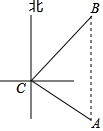 如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.
如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
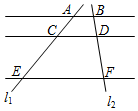 如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、C、E和点B、D、F,如果AC:CE=3:5,BF=9,那么DF=$\frac{45}{8}$.
如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、C、E和点B、D、F,如果AC:CE=3:5,BF=9,那么DF=$\frac{45}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
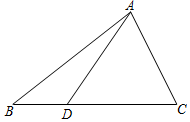 如图,已知点D是△ABC的边BC上一点,且BD=$\frac{1}{2}$CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,已知点D是△ABC的边BC上一点,且BD=$\frac{1}{2}$CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com