
如图,某建筑物BC顶部有釕一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.
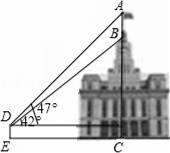

【考点】解直角三角形的应用-仰角俯角问题.
【分析】根据题意分别在两个直角三角形中求得AF和BF的长后求差即可得到旗杆的高度,进而求得BC的高度.
【解答】解:根据题意得DE=1.56,EC=21,∠ACE=90°,∠DEC=90°.
过点D作DF⊥AC于点F.
则∠DFC=90°∠ADF=47°,∠BDF=42°.
∵四边形DECF是矩形.
∴DF=EC=21,FC=DE=1.56,
在直角△DFA中,tan∠ADF=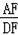
 ,
,
∴AF=DF•tan47°≈21×1.07=22.47(m).
在直角△DFB中,tan∠BDF=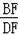
 ,
,
∴BF=DF•tan42°≈21×0.90=18.90(m),
则AB=AF﹣BF=22.47﹣18.90=3.57≈3.6(m).
BC=BF+FC=18.90+1.56=20.46≈20.5(m).
答:旗杆AB的高度约是3.6m,建筑物BC的高度约是20.5米.
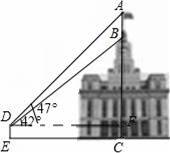

【点评】此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.


科目:初中数学 来源: 题型:
如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于
 AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )


A.矩形 B.菱形 C.正方形 D.等腰梯形
查看答案和解析>>
科目:初中数学 来源: 题型:
下面的说法正确的是( )
A.三角形的角平分线、中线和高都在三角形内
B.直角三角形的高只有一条
C.三角形的高至少有一条在三角形内
D.钝角三角形的三条高都在三角形外面
查看答案和解析>>
科目:初中数学 来源: 题型:
阳光通过窗口AB照射到室内,在地面上留下2.7米的亮区DE(如图所示),已知亮区到窗口下的墙角的距离EC=8.7米,窗口高AB=1.8米,则窗口底边离地面的高BC为( )
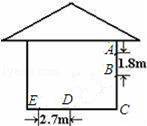

A.4米 B.3.8米 C.3.6米 D.3.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
一次函数y=﹣x+a﹣3(a为常数)与反比例函数y=﹣
 的图象交于A、B两点,当A、B两点关于原点对称时a的值是( )
的图象交于A、B两点,当A、B两点关于原点对称时a的值是( )
A.0 B.﹣3 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com