
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ����ĩ��ѧ����������ھ��꼶�����ȡ��һ����ѧ������ĩ��ѧ�ɼ�Ϊ��������Ϊ![]() ��
��![]() �֣���
�֣���![]() ��
��![]() �֣���
�֣���![]() ��
��![]() �֣���
�֣���![]() ��
��![]() �֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ����������⣺
�֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ����������⣺
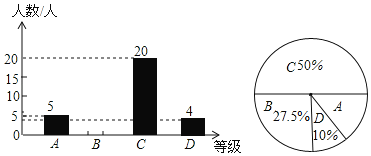
��1����������ȡ��ѧ�����ж����ˣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ѧУ���꼶����ѧ��![]() �ˣ�������Ϊ
�ˣ�������Ϊ![]() �֣���
�֣���![]() �֣�����Ϊ���㣬�������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ����Լ�ж��٣�
�֣�����Ϊ���㣬�������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ����Լ�ж��٣�
���𰸡���1��40�ˣ���2��ͼ����������3��480�ˣ�
��������
��1������![]() �ȼ�����������ռ�İٷֱ������������ȡ��ѧ������
�ȼ�����������ռ�İٷֱ������������ȡ��ѧ������
��2���ó�ȡ������������![]() �ȼ���ռ�İٷֱȣ��Ӷ���ȫͳ��ͼ��
�ȼ���ռ�İٷֱȣ��Ӷ���ȫͳ��ͼ��
��3���ø�У���꼶�����������������������ռ�İٷֱȣ����ɵó��𰸣�
�⣺��1����������ȡ��ѧ�����У�![]() ����
����![]() ��
��
��2��![]() �ȼ��������ǣ�
�ȼ��������ǣ�![]() �ˣ���ͼ��
�ˣ���ͼ��

��3����������ã�![]() ����
����![]() ��
��
����ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ��480�ˣ�


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Եȱ�������ABC��BC��Ϊֱ������Բ���ֱ�AB��AC�ڵ�E��D��DF��Բ�����ߣ�����F��BC�Ĵ��߽�BC�ڵ�G����AF�ij�Ϊ2����FG�ij�Ϊ
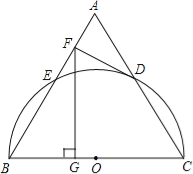
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��x2����a��x��bʱm��y��n��������˵����ȷ���ǣ�������
A.��n��m��1ʱ��b��a����Сֵ
B.��n��m��1ʱ��b��a�����ֵ
C.��b��a��1ʱ��n��m����Сֵ
D.��b��a��1ʱ��n��m�����ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BCΪֱ����Բ�ֱ�AC��AB��D��E���㣬����BD��DE����BDƽ�֡�ABC�������н��۲�һ���������ǣ�������
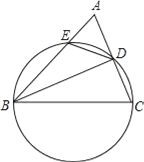
A. BD��AC B. AC2=2ABAE C. ��ADE�ǵ��������� D. BC=2AD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() (a��0)�ĶԳ���Ϊֱ��
(a��0)�ĶԳ���Ϊֱ��![]() ���������߾���A(1��0)��C(0��3)���㣬��
���������߾���A(1��0)��C(0��3)���㣬��![]() �ύ�ڵ�B��
�ύ�ڵ�B��
��1����ֱ��![]() ����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶԳ���![]() ����һ��M��ʹMA+MC��ֵ��С�����M�����ꣻ
����һ��M��ʹMA+MC��ֵ��С�����M�����ꣻ
��3����PΪ�����ߵĶԳ���![]() �ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
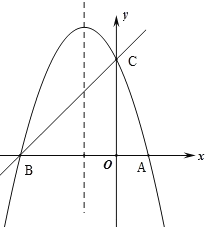
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C��
��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C��
(1)��������ߵĽ���ʽ��
(2)��ͼ�٣�����D����������һ���㣬���D�ĺ�����Ϊm��0��m��3��������CD��BD��BC��AC������BCD��������ڡ�AOC�����2��ʱ����m��ֵ��
(3)����NΪ�����߶Գ�����һ�㣬����ͼ����̽�����������Ƿ���ڵ�M��ʹ����B��C��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A(8��1)��B(0��3)������������![]() (x>0)��ͼ����A����ֱ��x=t(0<t<8)�뷴����������ͼ���ڵ�M����ֱ��AB���ڵ�N.
(x>0)��ͼ����A����ֱ��x=t(0<t<8)�뷴����������ͼ���ڵ�M����ֱ��AB���ڵ�N.
(1)��k��ֵ��
(2)����BMN��������ֵ��
(3)��MA��AB����t��ֵ.
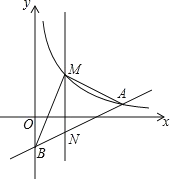
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ɽʤ����˾������һ���µĴ�����Ʒ��ÿ������Ʒ����ɱ�Ϊ18Ԫ���������̷��֣�ÿ������![]() ���
���![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���
֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���![]() ��
��
![]() д����˾ÿ�µ�����
д����˾ÿ�µ�����![]() ��Ԫ
��Ԫ![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ֮�亯������ʽ��
֮�亯������ʽ��
![]() �����۵���Ϊ����Ԫʱ����˾ÿ���ܹ�������������������Ƕ��٣�
�����۵���Ϊ����Ԫʱ����˾ÿ���ܹ�������������������Ƕ��٣�
![]() ���ݹ��̲��Ź涨�����ּ���Ʒ�����۵��۲��ø���32Ԫ
���ݹ��̲��Ź涨�����ּ���Ʒ�����۵��۲��ø���32Ԫ![]() �����˾Ҫ���ÿ�²�����350��Ԫ��������ô�������ּ���Ʒÿ�µ��������ɱ���Ҫ������Ԫ��
�����˾Ҫ���ÿ�²�����350��Ԫ��������ô�������ּ���Ʒÿ�µ��������ɱ���Ҫ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���![]() ����
����![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת����
˳ʱ����ת����![]() ����
����![]() ��
��![]() ��ת��Ķ�Ӧ��Ϊ
��ת��Ķ�Ӧ��Ϊ![]() ��
��![]() ������ת��Ϊ
������ת��Ϊ![]() ��
��
��1����ͼ�٣���![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��2����ͼ�ڣ���![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��3������![]() �����߶�
�����߶�![]() ���е�Ϊ
���е�Ϊ![]() ������
������![]() �����߶�
�����߶�![]() �ij�����Сֵ��ֱ��д��������ɣ���
�ij�����Сֵ��ֱ��д��������ɣ���
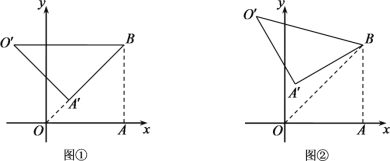
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com