
【题目】![]() 年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
商品 价格 | 甲 | 乙 |
进件(元 |
|
|
售价(元 |
|
|
该店有一批用![]() 元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共
元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共![]() 元.[毛利润
元.[毛利润![]() (售价
(售价![]() 进价)
进价)![]() 销售量]
销售量]


(1)该店库存的甲、乙两种手持红外测温枪分别为多少个?
(2)根据销售情况,该店计划增加甲种手持红外测温枪的购进量,减少乙种手持红外测温枪的购进量.已知甲种手持红外测温枪增加的数量是乙种手持红外测温枪减少的数量的![]() 倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过
倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过![]() 元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.
元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.
【答案】(1)甲种有![]() 个,乙种有
个,乙种有![]() 个.(2)该店用不超过
个.(2)该店用不超过![]() 元购进甲种手持红外测温枪
元购进甲种手持红外测温枪![]() 个,乙种手持红外测温枪
个,乙种手持红外测温枪![]() 个时,全部销售后获得的毛利润最大,最大毛利润为
个时,全部销售后获得的毛利润最大,最大毛利润为![]() 元.
元.
【解析】
(1)设该店库存手持红外线测温枪中甲种有![]() 个,乙种有
个,乙种有![]() 个.再根据等量关系用
个.再根据等量关系用![]() 元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共
元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共![]() 元列出方程组求解.
元列出方程组求解.
(2)设乙种手持红外测温枪减少![]() 个,则甲种手持红外测温枪增加
个,则甲种手持红外测温枪增加![]() 个,表示出购买的总资金,由总资金部超过40000元建立不等式就可以求出m的取值范围,再设销售后的毛利润为W元,表示出毛利润与m的关系式,由一次函数的性质就可以求出最毛大利润.
个,表示出购买的总资金,由总资金部超过40000元建立不等式就可以求出m的取值范围,再设销售后的毛利润为W元,表示出毛利润与m的关系式,由一次函数的性质就可以求出最毛大利润.
解:(1)设该店库存手持红外线测温枪中甲种有![]() 个,乙种有
个,乙种有![]() 个.
个.
由题意,得![]() .
.
解得![]()
答:该店库存手持红外线测温枪中甲种有![]() 个,乙种有
个,乙种有![]() 个.
个.
(2)设乙种手持红外测温枪减少![]() 个,则甲种手持红外测温枪增加
个,则甲种手持红外测温枪增加![]() 个.
个.
由题意,得![]() .
.
解得![]() .
.
设全部销售后获得的毛利润为![]() 元,由题意,得
元,由题意,得
![]() .
.
![]() ,
,
![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 当
当![]() 时,
时,![]() .
.
答:该店用不超过![]() 元购进甲种手持红外测温枪
元购进甲种手持红外测温枪![]() 个,乙种手持红外测温枪
个,乙种手持红外测温枪![]() 个时,全部销售后获得的毛利润最大,最大毛利润为
个时,全部销售后获得的毛利润最大,最大毛利润为![]() 元.
元.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
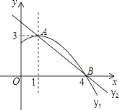
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
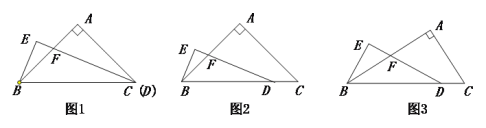
探究:当AB=AC且C,D两点重合时(如图1)探究:
(1)线段BE与FD之间的数量关系,直接写出结果 ;
(2)∠EBF= .
证明:当AB=AC且C,D不重合时,探究线段BE与FD的数量关系,并加以证明.
计算:当AB=![]() AC时,如图,求
AC时,如图,求![]() 的值 (用含
的值 (用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
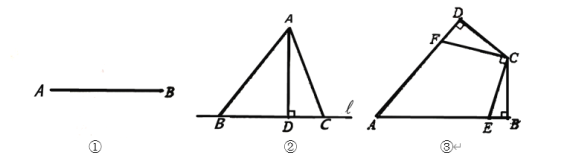
(1)如图①,已知线段AB,请以AB为斜边,在图中画出一个直角三角形;
(2)如图②,已知点A是直线l外一点,点B、C均在直线l上,AD⊥l且AD=3,∠BAC=60°,求△ABC面积的最小值;
问题解决
(3)如图③,某园林单位要设计把四边形花园划分为几个区域种植不同花草,在四边形ABCD中,∠A=45°,∠B=∠D=90°,CB=CD=6m,点E、F分别为AB、AD上的点,若保持CE⊥CF,那么四边形AECF的面积是否存在最大值?若存在,请求出面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
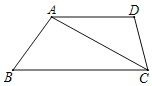
【题目】如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
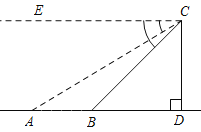
【题目】如图,直升飞机在大桥AB上方C点处测得A,B两点的俯角分别为45°和31°.若飞机此时飞行高度CD为1205m,且点A,B,D在同一条直线上,求大桥AB的长.(精确到1m)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
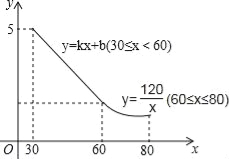
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
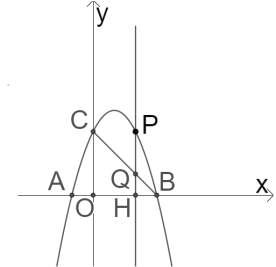
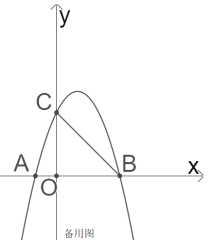
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C(0,3),点P是抛物线在第一象限上的一点,过点P作PH⊥x轴,垂足为H,交线段BC于点Q.
(1)求抛物线对应的函数表达式;
(2)当PQ=2QH时,求点P的坐标;
(3)当PH最大时,连接AP,AP与BC交于点D,点F是第一象限内一点,且∠AFC=45°,点G在抛物线上,直线FG、FC分别与直线PH交于点M、N.当三角形ABD相似三角形FMN时,求点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com