
【题目】在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF

(1)求证:∠E=∠C;
(2)如果DF平分∠AFB,求证:AC⊥AB
科目:初中数学 来源: 题型:
【题目】某市出租车计费办法如图所示.根据图象信息,下列说法错误的是( )

A. 出租车起步价是10元
B. 在3千米内只收起步价
C. 超过3千米部分(x>3)每千米收3元
D. 超过3千米时(x>3)所需费用y与x之间的函数关系式是y=2x+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长为 ![]() ,宽为
,宽为 ![]() 的大长方形被分割为
的大长方形被分割为 ![]() 小块,除阴影
小块,除阴影 ![]() ,
,![]() 外,其余
外,其余 ![]() 块是形状、大小完全相同的小长方形,其较短一边长为
块是形状、大小完全相同的小长方形,其较短一边长为 ![]() .
.

(1)每个小长方形较长的一边长是 ![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
(2)分别用含 ![]() ,
,![]() 的代数式表示阴影
的代数式表示阴影 ![]() ,
,![]() 的面积,并计算阴影 A 的面积与阴影B的面积的差.
的面积,并计算阴影 A 的面积与阴影B的面积的差.
(3)当 ![]() 时,阴影
时,阴影 ![]() 与阴影
与阴影 ![]() 的面积差会随着
的面积差会随着 ![]() 的变化而变化吗?请你作出判断,并说明理由.
的变化而变化吗?请你作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

解答下列问题:
(1)请用含![]() 、
、![]() 、
、![]() 的代数式表示大正方形的面积.
的代数式表示大正方形的面积.
方法1: ;方法2: .
(2)根据图2,利用图形的面积关系,推导![]() 、
、![]() 、
、![]() 之间满足的关系式.
之间满足的关系式.
(3)利用(2)的关系式解答:如果大正方形的面积是25,且![]() ,求小正方形的面积.
,求小正方形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-3与直线y=kx(k≠0)相交于点A和点B,则一元二次方程x2-kx-3=0的解的情况是( )

A. 有两个不相等的正实根 B. 有两个不相等的负实根
C. 一个正实根、一个负实根 D. 有两个相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有( )

A.2个B.3个C.4个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.

(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG=![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,![]() ,
,![]() ,
,![]() .
.
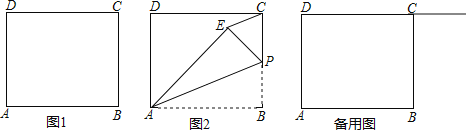
![]() 为边BC上一点,将
为边BC上一点,将![]() 沿直线AP翻折至
沿直线AP翻折至![]() 的位置
的位置![]() 点B落在点E处
点B落在点E处![]()
![]() 如图1,当点E落在CD边上时,利用尺规作图,在图1中作出满足条件的图形
如图1,当点E落在CD边上时,利用尺规作图,在图1中作出满足条件的图形![]() 不写作法,保留作图痕迹,用2B铅笔加粗加黑
不写作法,保留作图痕迹,用2B铅笔加粗加黑![]() 并直接写出此时
并直接写出此时![]() ______;
______;
![]() 如图2,若点P为BC边的中点,连接CE,则CE与AP有何位置关系?请说明理由;
如图2,若点P为BC边的中点,连接CE,则CE与AP有何位置关系?请说明理由;
![]() 点Q为射线DC上的一个动点,将
点Q为射线DC上的一个动点,将![]() 沿AQ翻折,点D恰好落在直线BQ上的点
沿AQ翻折,点D恰好落在直线BQ上的点![]() 处,则
处,则![]() ______;
______;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com