[题目]如图,抛物线y=x2-3与直线y=kx(k≠0)相交于点A和点B,则一元二次方程x2-kx-3=0的解的情况是( )A. 有两个不相等的正实根 B. 有两个不相等的负实根C. 一个正实根.一个负实根 D. 有两个相等的实数根题目和参考答案——青夏教育精英家教网—

【题目】如图,抛物线y=x2-3与直线y=kx(k≠0)相交于点A和点B,则一元二次方程x2-kx-3=0的解的情况是（）

A. 有两个不相等的正实根 B. 有两个不相等的负实根

C. 一个正实根、一个负实根 D. 有两个相等的实数根

【答案】C

【解析】

一元二次方程x2-kx-3=0可化为x2-3= kx ，由此可得一元二次方程x2-kx-3=0的解是抛物线y=x2-3与直线y=kx(k≠0)交点的横坐标，观察图象即可解答.

一元二次方程x2-kx-3=0可化为x2-3= kx ，由此可得一元二次方程x2-kx-3=0的解是抛物线y=x2-3与直线y=kx(k≠0)交点的横坐标，由图象可知，抛物线y=x2-3与直线y=kx(k≠0)交点的横坐标为一正一负，所以元二次方程x2-kx-3=0有一个正实根、一个负实根，故选C.

练习册系列答案

成功中考系统总复习系列答案

成长记寒假总动员云南科技出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某中学为了解学生到校交通方式情况，随机抽取各年级部分学生就“上下学交通方式”进行问卷调查，调查分为“A：骑自行车；B：步行；C：坐公交车；D：其他”四种情况，并根据调查结果绘制出部分条形统计图（如图①）和部分扇形统计图（如图②），请根据图中的信息，解答下列问题.

（1）本次调查共抽取名学生；

（2）求出扇形统计图中“C”所对扇形的圆心角的度数，并将条形统计图补充完整；

（3）若该中学共有学生3000人，估计有多少学生在上下学交通方式中选择坐公交车？

查看答案和解析>>

科目：初中数学 来源： 题型：

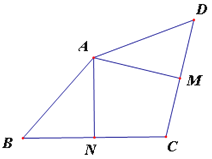
【题目】如图，在四边形ABCD中，M，N分别是CD，BC的中点，且AM⊥CD，AN⊥BC。

（1）求证：∠BAD=2∠MAN；

（2）连接BD，若∠MAN=70°，∠DBC=40°，求∠ADC。

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟．在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t

（分）之间的关系如图所示，下列结论：

①甲步行的速度为60米/分；

②乙走完全程用了30分钟；

③乙用16分钟追上甲；

④乙到达终点时，甲离终点还有320米

其中正确的结论有（　　）

A. 1 个B. 2 个C. 3 个D. 4 个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，对于点P (x，y)，若点Q的坐标为(ax+y，x+ay)，其中a为常数，则称点Q是点P的“a级关联点"，例如，点P(1，4)的“3级关联点"为Q (3×1+4，1+3×4)，即Q (7，13)。

(1)已知点A (-2，6)的“级关联点”是点A1，点B的“2级关联点”是B1 (3， 3)，求点A1和点B的坐标：

(2)已知点M (m-1， 2m)的“-3级关联点"M位于坐标轴上，求M的坐标

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在△ABC中，D为AB的中点，F为BC上一点，DF∥AC，延长FD至E，且DE=DF,联结AE、AF

（1）求证：∠E=∠C;

（2）如果DF平分∠AFB，求证：AC⊥AB

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图,抛物线y=-x2+x+与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.

(1)求点A,B,C的坐标;

(2)若该抛物线的顶点是点D,求四边形OCDB的面积;

(3)已知点P是该抛物线对称轴的一点,若以点P,O,D为顶点的三角形是等腰三角形,请直接写出点P的坐标.(不用说理)

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，为了测量出楼房AC的高度，从距离楼底C处米的点D（点D与楼底C在同一水平面上）出发，沿斜面坡度为i=1：的斜坡DB前进30米到达点B，在点B处测得楼顶A的仰角为53°，求楼房AC的高度（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈，计算结果用根号表示，不取近似值）．