Question

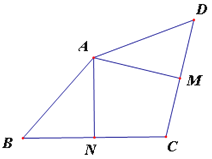
【题目】如图，在四边形ABCD中，M，N分别是CD，BC的中点，且AM⊥CD，AN⊥BC。

（1）求证：∠BAD=2∠MAN；

（2）连接BD，若∠MAN=70°，∠DBC=40°，求∠ADC。

Answer 1

【答案】（1）证明见解析；（2）50°

【解析】

（1）首先连接AC，根据AM⊥CD，AN⊥BC，判断出AM、AN分别是CD、BC的垂直平分线，得到AC＝AD，AB＝AC，再根据等腰三角形三线合一的性质得到∠DAM=∠CAM，∠BAN=∠CAN，然后根据角的和差即可得出结论；

（2）由∠MAN=70°，得出∠BAD的度数．由四边形ANCM内角和等于360°，得到∠BCD的度数．在△BCD中，由三角形内角和定理得到∠BDC的度数．在△ABD中，根据等腰三角形的性质和三角形内角和定理可得出∠ADB的度数，根据角的和差即可得出结论．

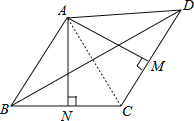
（1）如图，连接AC．

∵M、N分别是CD、BC的中点，且AM⊥CD，AN⊥BC，∴AM、AN分别是CD、BC的垂直平分线，∴AC＝AD，AB＝AC．

∵AM⊥CD，AN⊥BC，∴∠DAM=∠CAM，∠BAN=∠CAN，∴∠DAC+∠BAC=2∠CAM+2∠CAN，∴∠BAD=2∠MAN；

（2）∵∠MAN=70°，∴∠BAD=2∠MAN=140°．

∵AM⊥CD，AN⊥BC，∴∠BCD=180°－∠MAN=180°－70°=110°．

∵∠DBC=40°，∴∠BDC=180°－∠DBC－∠BCD=180°－40°－110°=30°．

∵AB=AC=AD，∴∠ABD=∠ADB．

∵∠BAD=140°，∴∠ABD=∠ADB=20°，∴∠ADC=∠ADB+∠BDC=20°+30°=50°．