
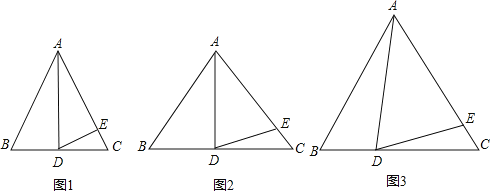
����Ŀ������ABC�У�AB=AC��
��1����ͼ1�������BAD=30����AD��BC�ϵĸߣ�AD=AE������EDC=
��2����ͼ2�������BAD=40����AD��BC�ϵĸߣ�AD=AE������EDC=
��3��˼����ͨ���������⣬�㷢����BAD����EDC֮����ʲô��ϵ������ʽ�ӱ�ʾ��
��4����ͼ3�����AD����BC�ϵĸߣ�AD=AE���Ƿ�����������ϵ�����У�����д��������˵�����ɣ�
���𰸡���1��15������2��20������3����EDC=![]() ��BAD����4���Գ���������������.
��BAD����4���Գ���������������.
��������
�����������1���������������ߺ�һ��������DAE=30��������ΪAD=AE��������ADE=��AED=75����������DEC=15����
��2��ͬ������֤��ADE=70����������DEC=20����
��3��ͨ����1����2����Ľ��ۿ�֪����BAD=2��EDC������EDC=![]() ��BAD����
��BAD����
��4������AD=AE��������ADE=��AED��������֪����֤��BAD+��B=2��EDC+��C����B=��C��������BAD=2��EDC��
�⣺��1��������ABC�У�AB=AC��AD��BC�ϵĸߣ�
���BAD=��CAD��
�ߡ�BAD=30����
���BAD=��CAD=30����
��AD=AE��
���ADE=��AED=75����
���EDC=15����
��2��������ABC�У�AB=AC��AD��BC�ϵĸߣ�
���BAD=��CAD��
�ߡ�BAD=40����
���BAD=��CAD=40����
��AD=AE��
���ADE=��AED=70����
���EDC=20����
��3����BAD=2��EDC������EDC=![]() ��BAD��
��BAD��
��4���Գ�������������
��AD=AE�����ADE=��AED��
���BAD+��B=��ADC=��ADE+��EDC=��AED+��EDC=����EDC+��C��+��EDC
=2��EDC+��C
����AB=AC��
���B=��C
���BAD=2��EDC��
�ʷֱ���15�㣬20�㣬��EDC=![]() ��BAD
��BAD


 �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��x��y���ڵ������ޣ��ҵ�P��x��ľ���Ϊ3����y��ľ���Ϊ2�����P�������ǣ� ��
A. ��-2��-3�� B. ��-2��3�� C. ��2��-3�� D. ��2��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=��x2+x+2����y��0ʱ���Ա���x��ȡֵ��Χ�ǣ� ��
A��x����1��x��2 B����1��x��2
C��x����2��x��1 D����2��x��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ÿ��С�����εı߳�Ϊ1����A������Ϊ����3��2�����밴Ҫ��ֱ�������и�С�⣺
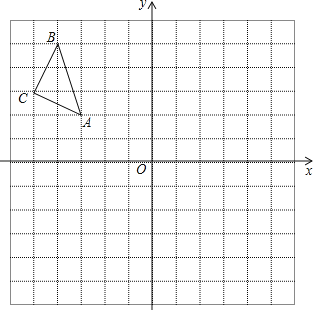
��1������ABC����ƽ��4����λ�õ���A1B1C1��������A1B1C1����A1�������� ��
��2��������ABC����y��ԳƵ���A2B2C2����C2�������� ��
��3������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʹ����ֱ��������ȫ�ȵ�������( )
A. ��ֱ�DZ߶�Ӧ��� B. һ��Ƕ�Ӧ���
C. ����Ƕ�Ӧ��� D. б�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4��AD=5��AD��AB��BC�ֱ�����O������E��F��G���㣬����D����O������BC�ڵ�M���е�ΪN����DM�ij�Ϊ�� ��
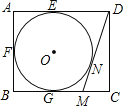
A��![]() B��
B��![]() C��
C��![]()
![]() D��2
D��2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ֱ��y=3x+3��x�ύ��C�㣬��y�ύ��A�㣬B����x���ϣ���OAB�ǵ���ֱ�������Σ�

��1�����A��B��C����������ߵĽ���ʽ��
��2����ֱ��CD��AB����������D�㣬��D������ꣻ
��3����P�����������ϵĶ��㣬���ڵ�һ���ޣ���ô��PAB�Ƿ��������������У������ʱP����������PAB������������û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x����̣�3xn-1+��m-2��x2 = 5��һԪһ�η��̣���m =_____n =__
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������г��ȵ������߶��У�����������ε��ǣ�������
A. 3��7��15 B. 1��2��4 C. 5��5��10 D. 2��3��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com