

分析 (1)由于∠AEF=90°,故∠FEC=∠EAB,而E是BC中点,从而只需取AB点G,连接EG,则有AG=CE,BG=BE,∠AGE=∠ECF,易得△AGE≌△ECF;
(2)①由于AB=BC,所以只要AG=EC就有BG=BE,就同样可得△AGE≌△ECF,于是截取AG=EC,证全等即可;
②根据A、D两点的坐标求出抛物线解析式,设出F点的横坐标,纵坐标用横坐标表示,将F点的坐标代入抛物线解析式即可求出坐标.
解答 解:(1)如图1,取AB的中点G,连接EG.△AGE≌△ECF.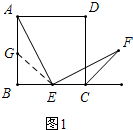
(2)①若点E在线段BC上滑动时AE=EF总成立.
证明:如图2,在AB上截取AG=EC.
∵AB=BC,
∴BG=BE,
∴△GBE是等腰直角三角形,
∴∠AGE=180°-45°=135°,
∵CF平分正方形的外角,
∴∠ECF=135°,
∴∠AGE=∠ECF,
而∠BAE+∠AEB=∠CEF+∠AEB=90°,
∴∠BAE=∠CEF,
∴△AGE≌△ECF,
∴AE=EF.
②由题意可知抛物线经过A(0,1),D(1,1)两点,
∴$\left\{\begin{array}{l}{a+1+c=1}\\{c=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{c=1}\end{array}\right.$,
∴抛物线解析式为y=-x2+x+1,
过点F作FH⊥x轴于H,
由①知,FH=BE=CH,设BH=a,则FH=a-1,
∴点F的坐标为F(a,a-1),
∵点F恰好落在抛物线y=-x2+x+1上,
∴a-1=-a2+a+1,
∴a=$\sqrt{2}$(负值不合题意,舍去),
点F的坐标为F($\sqrt{2}$,$\sqrt{2}-1$)..
点评 本题主要考查了正方形的性质、全等等三角形的判定与性质、待定系数法求二次函数解析式等知识点,难度不大,属于中档题.在构造全等三角形时,要先明确已经具备哪些相等条件,还缺什么条件,然后结合全等三角形的判定定理很容易作出辅助线.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
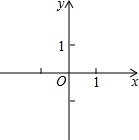 P1(x1,y1),P2(x2,y2)是平面直角坐标系中的任意两点,我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的“直角距离”,记作d(P1,P2).
P1(x1,y1),P2(x2,y2)是平面直角坐标系中的任意两点,我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的“直角距离”,记作d(P1,P2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款不少于15元的有( )
如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款不少于15元的有( )| A. | 40人 | B. | 32人 | C. | 20人 | D. | 12人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com