
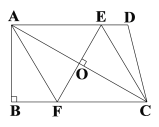
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由于知道了EF垂直平分AC,因此只要证出四边形AFCE是平行四边形即可得出AFCE是菱形的结论.
(2)根据勾股定理得出AC,进而利用勾股定理解答即可.
证明:(1)∵EF是对角线AC的垂直平分线,
∴AO=CO,AC⊥EF,
∵AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
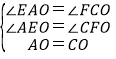 ,
,
∴△AEO≌△CFO(AAS),
∴AE=CF,
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠B=90°,AB=6,BC=8,
∴AC= ![]() ,
,
∵四边形AFCE是菱形,
∴AF=FC,
在Rt△ABF中,设AF=FC=x,则BF=8-x
∴AB2+BF2=AF2,
∴62+(8-x)2=x2,
∴x=![]() ,
,
∴OF ![]() ,
,
∴EF=2OF=![]() .
.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成不完整的统计表,请根据图表中的信息解答下列问题.
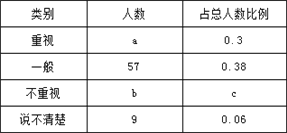
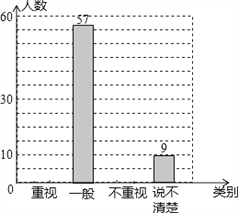
(1)样本容量为 ,表格中c的值为 ,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数为 ;
(3)根据上面的数据统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
如图、![]() 与
与![]() 互补,
互补,![]() ,求证:
,求证:![]() .对于本题小丽是这样证明的,请你将她的证明过程补充完整.
.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
证明:![]() 与
与![]() 互补,(已知)
互补,(已知)
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
![]() ,(已知)
,(已知)
![]() ,(等量代换)
,(等量代换)
即_______________=_______________.
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠BAC=60°,点P为边BC的中点,分别以AB和AC为斜边向外作Rt△ABD和Rt△ACE,且∠DAB=∠EAC=α,连结PD,PE,DE.
(1)如图1,若α=45°,则![]() = ;
= ;
(2)如图2,若α为任意角度,求证:∠PDE=α;
(3)如图3,若α=15°,AB=8,AC=6,则△PDE的面积为 .
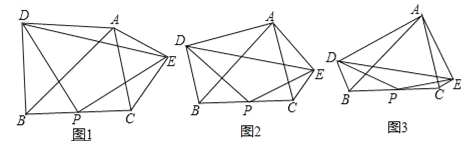
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=x2﹣2x(x≥0)的图象沿y轴翻折得到一个新的图象,前后两个图象其实就是函数y=x2﹣2|x|的图象.
(1)观察思考
函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;方程x2﹣2|x|=2有 个实数根;关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 ;
(2)拓展探究
①如图2,将直线y=x+1向下平移b个单位,与y=x2﹣2|x|的图象有三个交点,求b的值;
②如图3,将直线y=kx(k>0)绕着原点旋转,与y=x2﹣2|x|的图象交于A、B两点(A左B右),直线x=1上有一点P,在直线y=kx(k>0)旋转的过程中,是否存在某一时刻,△PAB是一个以AB为斜边的等腰直角三角形(点P、A、B按顺时针方向排列).若存在,请求出k值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为﹣7,﹣1,3,乙袋中的三张卡片上所标的数值分别为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上标的数值,把x、y分别作为点A的横坐标、纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况;
(2)求点A落在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com