
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.

【答案】(1)四边形ACGD为平行四边形,理由见解析;(2)证明见解析.
【解析】
(1)利用等腰直角三角形的性质易得BD=2BC,因为G为BD的中点,可得BG=BC,由∠CGB=45°,∠ADB=45°得AD∥CG,由∠CBD+∠ACB=180°,得AC∥BD,得出四边形ACGD为平行四边形;
(2)利用全等三角形的判定证得△DAC≌△BAE,由全等三角形的性质得BE=CD;首先证得四边形ABCE为平行四边形,再利用全等三角形的判定定理得△BCE≌△CAD,易得∠CBE=∠ACD,由∠ACB=90°,易得∠CFB=90°,得出结论.
(1)解:∵△ABC是等腰直角三角形,∠ACB=90°,
∴AB=![]() BC,
BC,
∵△ABD和△ACE均为等腰直角三角形,
∴BD=![]() =
=![]() =2BC,
=2BC,
∵G为BD的中点,
∴BG=![]() BD=BC,
BD=BC,
∴△CBG为等腰直角三角形,
∴∠CGB=45°,
∵∠ADB=45°,
AD∥CG,
∵∠ABD=45°,∠ABC=45°
∴∠CBD=90°,
∵∠ACB=90°,
∴∠CBD+∠ACB=180°,
∴AC∥BD,
∴四边形ACGD为平行四边形;
(2)证明:∵∠EAB=∠EAC+∠CAB=90°+45°=135°,
∠CAD=∠DAB+∠BAC=90°+45°=135°,
∴∠EAB=∠CAD,
在△DAC与△BAE中,
 ,
,
∴△DAC≌△BAE,
∴BE=CD;
∵∠EAC=∠BCA=90°,EA=AC=BC,
∴四边形ABCE为平行四边形,
∴CE=AB=AD,
在△BCE与△CAD中,
 ,
,
∴△BCE≌△CAD,
∴∠CBE=∠ACD,
∵∠ACD+∠BCD=90°,
∴∠CBE+∠BCD=90°,
∴∠CFB=90°,
即BE⊥CD.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
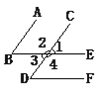
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图. 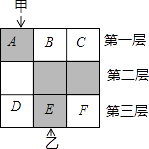
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动. ①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一快递小哥骑电动车需要在规定的时间把快递送到某地,若他以![]() 的速度行驶就会提前2分钟到达,如果他以
的速度行驶就会提前2分钟到达,如果他以![]() 的速度行驶就要迟到6分钟。
的速度行驶就要迟到6分钟。
(1)快递小哥行驶的路程是多少千米;
(2)当快递小哥以![]() 的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。
的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时50分,逆风飞行需要3小时.
(1)求无风时飞机的飞行速度;
(2)求两城之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是_____(用字母n表示).
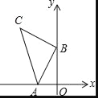
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com