
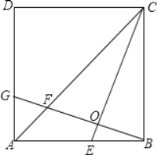
【题目】如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.
(1)证明:BE=AG;
(2)E位于什么位置时,∠AEF=∠CEB?说明理由.
【答案】(1)见解析;(2)当点E位于线段AB中点时,∠AEF=∠CEB ,理由见解析
【解析】
(1) 根据正方形的性质利用ASA判定△GAB≌△EBC,根据全等三角形的对应边相等可得到AG=BE;
(2) 利用SAS判定△GAF≌△EAF,从而得到∠AGF=∠AEF,由△GAB≌△EBC可得到∠AGF=∠CEB,则∠AEF=∠CEB.
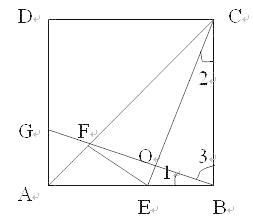
(1)证明:∵四边形ABCD是正方形
∴∠ABC=∠BAD=90°,∴∠1+∠3=90°,
∵BG⊥CE,∴∠BOC=90°∴∠2+∠3=90°,
∴∠1=∠2,
在△GAB和△EBC中,
∵∠GAB=∠EBC=90°,AB=BC,∠1=∠2,
∴△GAB≌△EBC (ASA) ,
∴AG=BE;
(2)解:当点E位于线段AB中点时,∠AEF=∠CEB ,
理由如下:若当点E位于线段AB中点时,则AE=BE,
由(1)可知,AG=BE,
∴AG=AE,
∵四边形ABCD是正方形,
∴∠GAF=∠EAF=45°,
又∵AF=AF,
∴△GAF≌△EAF (SAS),
∴∠AGF=∠AEF,
由(1)知,△GAB≌△EBC,
∴∠AGF=∠CEB,
∴∠AEF=∠CEB.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠CAB=60,BC的长为![]() ,求四边形OCED的周长
,求四边形OCED的周长

查看答案和解析>>
科目:初中数学 来源: 题型:
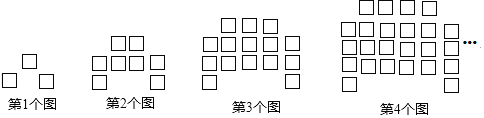
【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
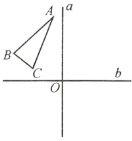
【题目】如图所示,已知![]() 和互相垂直的两条直线
和互相垂直的两条直线![]() 、
、![]() ,垂足为点
,垂足为点![]() .
.![]() 与
与![]() 关于直线
关于直线![]() 成轴对称,
成轴对称,![]() 与
与![]() 关于直线
关于直线![]() 成对称.那么下列说法正确的是( )
成对称.那么下列说法正确的是( )
A.![]() 可以由
可以由![]() 平移得到B.
平移得到B.![]() 可以由
可以由![]() 翻折得到
翻折得到
C.![]() 与
与![]() 成轴对称D.
成轴对称D.![]() 与
与![]() 成中心对称
成中心对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“迎新年”为主题的艺术活动,举办了四个项目的比赛.它们分别是:A演讲、B唱歌、C书法、D绘画.要求每位同学必须参加且限报一项.以九(一)班为样本进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给出的信息解答下列问题:
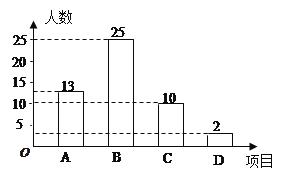
(1)求出参加绘画比赛的学生人数占全班总人数的百分比;
(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数;

(3)若该校九年级学生共有500人,请你估计这次活动中参加演讲和唱歌的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年6月28日,深湛高铁正式运营.从湛江到广州全程约468km,高铁开通后,运行时间比特快列车所用的时间减少了6h.若高铁列车的平均速度是特快列车平均速度的3倍,求特快列车与高铁的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com