
【题目】如图,在□ ![]() 中,过点
中,过点 ![]() 作
作 ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,
, ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,
, ![]() .
.
求证:四边形 ![]() 是菱形.
是菱形.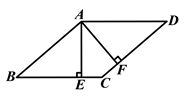
【答案】证明:连接 ![]() ,如图.
,如图.
∵ ![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,
, ![]() ,
,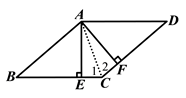
∴ ![]() .
.
∵四边形 ![]() 是平行四边形,
是平行四边形,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴□ ![]() 是菱形.
是菱形.
证法二:
∵四边形 ![]() 是平行四边形,如图2.
是平行四边形,如图2.
∴ ![]() .
.
∵ ![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,
,
∴ ![]() .
.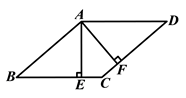
又∵ ![]() ,
,
∴ ![]() ≌
≌ ![]() .
.
∴ ![]() .
.
∴□ ![]() 是菱形.
是菱形.
证法三:
∵四边形 ![]() 是平行四边形,如图2.
是平行四边形,如图2.![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴□ ![]() 是菱形.
是菱形.
【解析】方法一:连接AC,由E⊥BC,AF⊥DC,AE=AF,可得∠2=∠1,再由平行线的性质和等腰三角形的判定可证得DA=DC,即可得□ABCD是菱形;方法二:根据已知条件易证△AEB≌△AFD,可得AB=AD,所以□ABCD是菱形;方法三:由平行四边形的面积S=BCAE=CDAF,即可证得BC=CD,所以□ABCD是菱形.
【考点精析】通过灵活运用等腰三角形的判定和平行四边形的性质,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图是甲、乙两公司近年销售收入情况的折线统计图,根据统计图得出下列结论,其中正确的是( )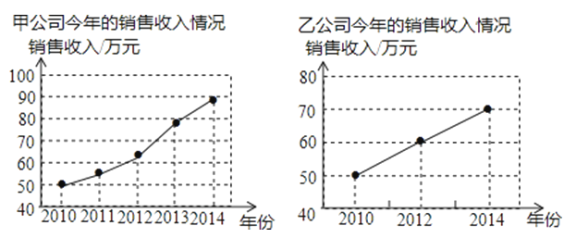
A.甲公司近年的销售收入增长速度比乙公司快
B.乙公司近年的销售收入增长速度比甲公司快
C.甲、乙两公司近年的销售收入增长速度一样快
D.不能确定甲、乙两公司近年销售收入增长速度的快慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2﹣2mx(m>1)与x轴的另一个交点为A.过点P(﹣1,m)作直线PD⊥x轴于点D,交抛物线于点B,BC∥x轴交抛物线于点C.

(1)当m=2时.
①求线段BC的长及直线AB所对应的函数关系式;
②若动点Q在直线AB上方的抛物线上运动,求点Q在何处时,△QAB的面积最大?
③若点F在坐标轴上,且PF=PC,请直接写出符合条件的点F在坐标;
(2)当m>1时,连接CA、CP,问m为何值时,CA⊥CP?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在双曲线上,AD垂直![]() 轴,垂足为
轴,垂足为
A,点C在AD上,CB平行于![]() 轴交双曲线于点B,直线AB与
轴交双曲线于点B,直线AB与![]() 轴交于点F,已知AC:
轴交于点F,已知AC:
AD=1:3,点C的坐标为(2,2)。
(1)求该双曲线的解析式;
(2)求△OFA的面积。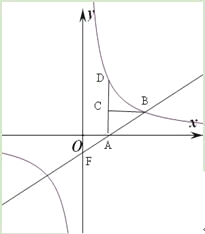
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 两条不相交的直线叫做平行线
B. 一条直线的平行线有且只有一条
C. 若直线a∥b,a∥c,则b∥c
D. 若两条线段不相交,则它们互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,我们曾经研究过![]() 的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道:
的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道: ![]() …
…![]() 时,我们可以这样做:
时,我们可以这样做:
(1)观察并猜想:
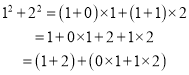 ;
;
![]()
=![]()
=![]() ;
;
![]()
=![]()
=![]() ( );…
( );…
(2)归纳结论:
![]() …
…![]() …
…![]()
=![]() …
…![]()
=( )+[ ]
= +
=![]() .
.
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=![]() ,求EF的长和半径OA的长.
,求EF的长和半径OA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
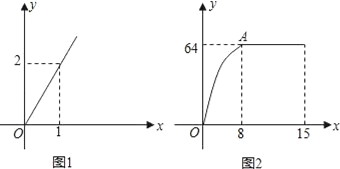
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com