
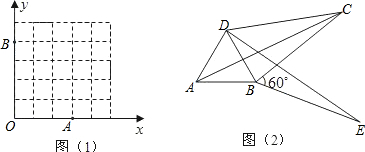
分析 (1)根据定义和勾股四边形的性质,有矩形或正方形或直角梯形满足题意;
(2)OM=AB知以格点为顶点的M共两个,分别得出答案;
(3)连接CE,证明△BCE是等边三角形,△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形;
(4)连接CE,证明△DCE是直角三角形,继而可证明四边形ABCD是勾股四边形.
解答  解:(1)学过的特殊四边形中是勾股四边形的两种图形的名称:矩形,正方形;
解:(1)学过的特殊四边形中是勾股四边形的两种图形的名称:矩形,正方形;
故答案为:矩形,正方形;
(2)如图1所示:M(3,4),M(4,3);
(3)证明:如图2,连接CE,由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,又
∵∠CBE=60,
∴△CBE为等边三角形,
∴BC=CE,∠BCE=60,
∵∠DCB=30,
∴∠DCE=∠DCB+∠BCE=30°+60°=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形.
(4)如图3,当∠DCB=$\frac{α}{2}$,四边形ABCD是勾股四边形,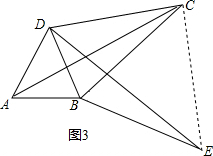 理由:连接CE,
理由:连接CE,
由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
又∵∠CBE=α,
∴∠BCE=∠BEC=90°-$\frac{α}{2}$,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形
故答案为:$\frac{a}{2}$.
点评 本题考查了四边形的综合以及勾股定理旋转的性质等知识,解答本题的关键是仔细审题,了解勾股四边形的定义及性质,难点在第四问,注意等量代换法的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4<a<16 | B. | 14<a<26 | C. | 12<a<20 | D. | 8<a<32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
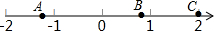 如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,再直爬向C点停止,已知点A表示-$\sqrt{2}$,点C表示2,设点B所表示的数为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com