
| A. | 2<$\sqrt{6}$<$\root{3}{7}$ | B. | 2<$\root{3}{7}$<$\sqrt{6}$ | C. | $\root{3}{7}$<2$<\sqrt{6}$ | D. | $\root{3}{7}$<$\sqrt{6}$<2 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).
问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请在所给网格中按下列要求操作:
请在所给网格中按下列要求操作:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
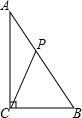 如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )| A. | 5 | B. | 5或8 | C. | $\frac{5}{2}$ | D. | 4或$\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5与5 | B. | -5与$\frac{1}{5}$ | C. | -5与-$\frac{1}{5}$ | D. | -5与|-5| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com