
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.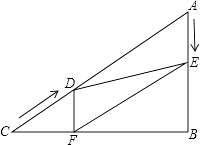
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
【答案】
(1)
证明:∵RT△ABC中,∠B=90°,∠A=60°,
∴∠C=90°﹣∠A=30°.
又∵在RT△CDF中,∠C=30°,CD=4t
∴DF= ![]() CD=2t,
CD=2t,
∴DF=AE
(2)
解:∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,解得:t=10,
即当t=10时,四边形AEFD是菱形
(3)
解:四边形BEDF不能为正方形,理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t= ![]() 时,∠EDF=90°
时,∠EDF=90°
但BF≠DF,
∴四边形BEDF不可能为正方形
【解析】(1)由已知条件可得RT△CDF中∠C=30°,即可知DF= ![]() CD=AE=2t;(2)由(1)知DF∥AE且DF=AE,即四边形ADFE是平行四边形,若构成菱形,则邻边相等即AD=AE,可得关于t的方程,求解即可知;(3)四边形BEDF不为正方形,若该四边形是正方形即∠EDF=90°,即DE∥AB,此时AD=2AE=4t,根据AD+CD=AC求得t的值,继而可得DF≠BF,可得答案.
CD=AE=2t;(2)由(1)知DF∥AE且DF=AE,即四边形ADFE是平行四边形,若构成菱形,则邻边相等即AD=AE,可得关于t的方程,求解即可知;(3)四边形BEDF不为正方形,若该四边形是正方形即∠EDF=90°,即DE∥AB,此时AD=2AE=4t,根据AD+CD=AC求得t的值,继而可得DF≠BF,可得答案.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
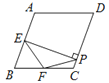
A. 55° B. 50° C. 45° D. 35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m. 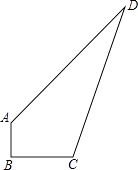
(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. 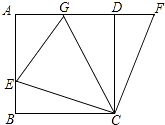
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师给42名学生每人买了一件纪念品,其中有:每支12元的钢笔,每把4元的圆规,每册16元的词典,共用了216元,则陈老师买了钢笔支,词典册;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣mx﹣2m2=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若x=1是该方程的根,求代数式4m2+2m+5的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.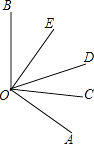
(1)若∠AOB=120°,则∠COE是多少度?
(2)若∠EOC=65°,∠DOC=25°,则∠BOE是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com