
【题目】如图,利用我们现在已经学过的圆和锐角三角函数的知识可知,半径 r 和圆心角θ及其所对的弦长 l之间的关系为![]() ,从而
,从而![]()
![]() ,综合上述材料当
,综合上述材料当![]() 时,
时,![]() ______.
______.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤.问雀、燕每
斤.问雀、燕每![]() 只各重多少斤?”
只各重多少斤?”
请列方程组解答上面的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() (-1,0)、
(-1,0)、![]() ,与
,与![]() 轴交于点
轴交于点![]() (0,4),连接
(0,4),连接![]() 、
、![]() ,且抛物线的对称轴为直线
,且抛物线的对称轴为直线![]() .
.
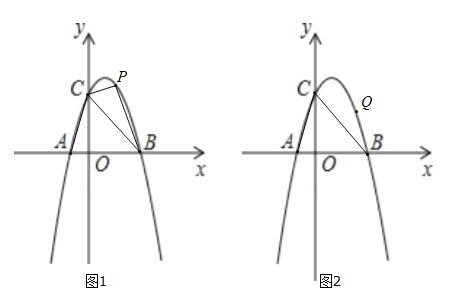
(1)求二次函数的解析式;
(2)若点![]() 是抛物线在一象限内
是抛物线在一象限内![]() 上方一动点,且点
上方一动点,且点![]() 在对称轴的右侧,连接
在对称轴的右侧,连接![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(3)如图2,若点![]() 是抛物线上一动点,且满足
是抛物线上一动点,且满足![]() ,请直接写出点
,请直接写出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
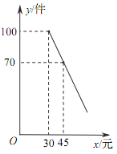
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD 为⊙O 的直径,弦 AB 交 CD 于点E,连接 BD、OB.

(1)求证:△AEC∽△DEB;
(2)若 CD⊥AB,AB=6,DE=1,求⊙O 的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某交为了开展“阳光体育运动”,计划购买篮球和足球,已知足球的单价比篮球的单价多![]() 元.若购买
元.若购买![]() 个篮球和
个篮球和![]() 个足球需花费
个足球需花费![]() 元.
元.
(1)求篮球和足球的单价各是多少元;
(2)若学校购买篮球和足球共![]() 个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
个,且购买篮球的总金额不超过购买足球的总金额,则学校最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
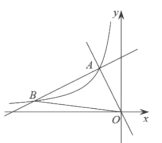
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.
(1)如图1,求证:∠CAE=∠CBD;
(2)如图2,F是BD的中点,求证:AE⊥CF;
(3)如图3,F,G分别是BD,AE的中点,若AC=2![]() ,CE=1,求△CGF的面积.
,CE=1,求△CGF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com