
【题目】如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.

【答案】△AED≌△CFB,详见解析
【解析】
根据平行四边形的性质可得DA=BC,DA∥BC,根据平行线的性质可得∠DAC=∠BCA,进而可判定△AED≌△CFB.然后可得DE=BF,再证明△DEC≌△BFA,再利用SSS证明△ADC≌△CBA即可.
△AED≌△CFB;
∵四边形ABCD是平行四边形,
∴DA=BC,DA∥BC,CD=AB,
∴∠DAC=∠BCA,
在△AED和△CFB中 ,
,
∴△AED≌△CFB(SAS).
∴DE=BF,
∵AE=CF,
∴AE+EF=CF+EF,
∴AF=CE,
在△DEC和△BFA中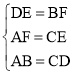 ,
,
∴△DEC≌△BFA(SSS),
在△ADC和△CBA中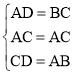 ,
,
∴△ADC≌△CBA(SSS).



科目:初中数学 来源: 题型:
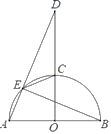
【题目】如图,已知AB是半圆O的直径,OC⊥AB交半圆于点C,D是射线OC上一点,连结AD交半圆O于点E,连结BE,CE.
(1)求证:EC平分∠BED.
(2)当EB=ED时,求证:AE=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
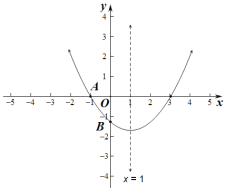
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() (-1,0),与
(-1,0),与![]() 轴的交点在
轴的交点在![]() (0,-2)和(0,-1)之间(不包括这两点),对称轴为直线
(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为(_______).
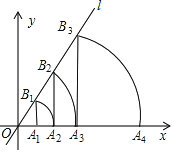
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用我们现在已经学过的圆和锐角三角函数的知识可知,半径 r 和圆心角θ及其所对的弦长 l之间的关系为![]() ,从而
,从而![]()
![]() ,综合上述材料当
,综合上述材料当![]() 时,
时,![]() ______.
______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地有一个直径为 14 米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心 2 米处达到最高,高度为5米 ,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示以水平方向为 x 轴,喷水池中心为原点建立直角坐标系.
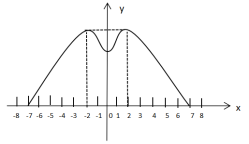
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高 1.8 米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估规划,政府决定对喷水设施改造成标志性建筑,做出如下设计改进;在喷出水柱的形状不变的前提下,把水池的直径扩大到 42 米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的顶点坐标为(2,0),直线y = x+1与二次函数的图象交于A、B两点,其中点A在y轴上.
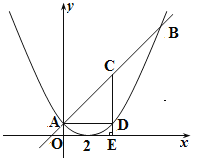
(1)二次函数的解析式为y = ;
(2)证明点(-m,2m-1)不在(1)中所求的二次函数图象上;
(3)若C为线段AB的中点,过点C做CE⊥x轴于点E,CE与二次函数的图象交于D.
①y轴上存在点K,使K、A、D、C为顶点的四边形是平行四边形,则点K的坐标是 .
②二次函数的图象上是否存在点P,使得三角形 S△ POE=2S△ABD?若存在,求出P坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com