
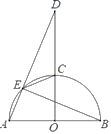
【题目】如图,已知AB是半圆O的直径,OC⊥AB交半圆于点C,D是射线OC上一点,连结AD交半圆O于点E,连结BE,CE.
(1)求证:EC平分∠BED.
(2)当EB=ED时,求证:AE=CE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由AB是半圆O的直径,得到∠AEB=90°,求得∠DEB=90°.再根据圆周角定理得出∠BEC=![]() 45°从而推出∠BEC=∠DEC,于是得到结论;
45°从而推出∠BEC=∠DEC,于是得到结论;
(2)连结BC根据全等三角形的性质得到∠CBE=∠CDE.根据圆周角定理得到∠AOE=∠COE,于是得到AE=CE.
解:(1)∵AB是半圆O的直径,
∴∠AEB=90°,
∴∠DEB=90°.
∵OC⊥AB,
∴∠AOC=∠BOC=90°,
∴∠BEC=45°,
∴∠DEC=45°.
∴∠BEC=∠DEC,
即EC平分∠BEC;
(2)连结BC,OE,
∵BE=DE,∠BEC=∠DEC,EC=EC,
在△BEC与△DEC中,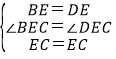 ,
,
∴△BEC≌△DEC,
∴∠CBE=∠CDE.
∵∠CDE=90°﹣∠A=∠ABE,
∴∠ABE=∠CBE.
∵∠AOE=2∠ABE,∠COE=2∠CBE.
∴∠AOE=∠COE,
∴AE=CE.


科目:初中数学 来源: 题型:
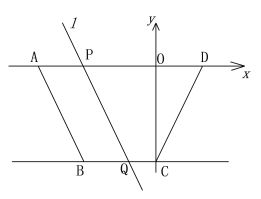
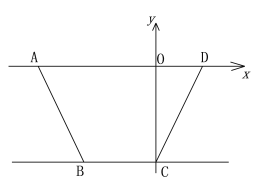
【题目】如图,已知四边形ABCD中,AD∥BC,BC=3,边AD在x轴上,点C在y轴上,点D坐标为(2,0),直线l:y=-2x-10经过点A、B.
(1)求四边形ABCD的面积;
(2)将直线l向右平移,平移后的直线与x轴交于点P,与直线BC交于点Q,设AP=t.直线l在平移过程中,是否存在t的值,使△PDQ为等腰三角形?若存在,求出t的值,若不存在,请说明理由;
(3)将直线l绕点A旋转,当直线l将四边形ABCD的面积分为1:3两部分时,请直接写出l与BC的交点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
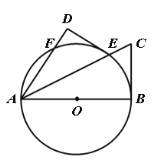
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”
译文:“今有![]() 只雀、
只雀、![]() 只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.
只燕,分别聚焦而且用衡器称之,聚在一起的雀重,燕轻.经一只雀、一只燕交换位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量为
只燕重量为![]() 斤.问雀、燕每
斤.问雀、燕每![]() 只各重多少斤?”
只各重多少斤?”
请列方程组解答上面的问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=ax2(a≠0)与一次函数y=kx+b的图象相交于A(﹣1,﹣1),B(2,﹣4)两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点.
(1)请直接写出a,k,b的值及关于x的不等式ax2<kx﹣2的解集;
(2)当点P在直线AB上方时,请求出△PAB面积的最大值并求出此时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,请直接写出P,Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com