
【题目】如图,CD 为⊙O 的直径,弦 AB 交 CD 于点E,连接 BD、OB.

(1)求证:△AEC∽△DEB;
(2)若 CD⊥AB,AB=6,DE=1,求⊙O 的半径长.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)经过点(﹣1,0),且满足4a+2b+c>0,有下列结论:①a+b>0;②﹣a+b+c>0;③b2﹣2ac>5a2.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,5个福娃2枚徽章145元,10个福娃3枚徽章280元(5个福娃为1套),则:
(1)一套“福娃”玩具和一枚徽章的价格各是多少元?
(2)买5套“福娃”玩具和10枚徽章共需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用我们现在已经学过的圆和锐角三角函数的知识可知,半径 r 和圆心角θ及其所对的弦长 l之间的关系为![]() ,从而
,从而![]()
![]() ,综合上述材料当
,综合上述材料当![]() 时,
时,![]() ______.
______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人自主学习的选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
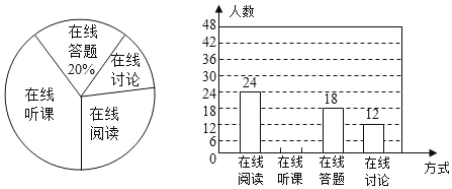
请你根据统计图中提供的信息解答下列问题:
(1)求本次调查的学生总人数;
(2)通过计算补全条形统计图;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生有多少人.
人,请你估计该校对在线阅读最感兴趣的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
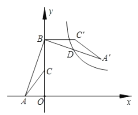
【题目】如图,点 A 的坐标是(﹣2,0),点 B 的坐标是(0,6),C 为 OB 的中点,将△ABC 绕点 B 逆时针旋转 90°后得到△A′B′C′.若反比例函数 y ![]() 的图象恰好经过 A′B 的中点 D,则k _________.
的图象恰好经过 A′B 的中点 D,则k _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=-![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),交y轴于点C.将直线AC以点A为旋转中心,顺时针旋转90°,交y轴于点D,交拋物线于另一点E.
与x轴交于A、B两点(点A在点B的左侧),交y轴于点C.将直线AC以点A为旋转中心,顺时针旋转90°,交y轴于点D,交拋物线于另一点E.
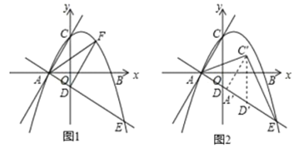
(1)求直线AE的解析式;
(2)点F是第一象限内抛物线上一点,当△FAD的面积最大时,求出此时点F的坐标;
(3)如图2,将△ACD沿射线AE方向以每秒![]() 个单位的速度平移,记平移后的△ACD为△A′C′D′,平移时间为t秒,当△AC′E为等腰三角形时,求t的值.
个单位的速度平移,记平移后的△ACD为△A′C′D′,平移时间为t秒,当△AC′E为等腰三角形时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com