
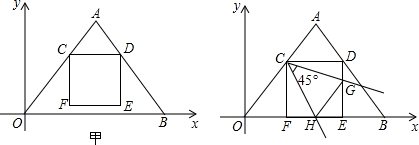
���� ��1�����ȿ��ǵ�F��OB��ʱ����Ӧ��S��t��ֵ��Ȼ��ֱ�Ե�F�ڡ�OAB�ڲ����ⲿ�������ۣ��Ϳɽ�����⣮
��2�����ڡ�OCFΪ����������ʱ������ȷ������˿ɷ������������FO=FC����CO=CF����OC=OF���������ۣ�ֻ������߶�֮���������ϵ��������t�ķ��̣��Ϳɽ�����⣻
��3����x���Ͻ�ȡFM=DG������CM�������ı���CDEF�������Σ��õ�CD=CF����CDE=��CFE=��CFM=��FCD=90�㣬֤����CFM�ա�CDG�����ǵõ���DCG=��MCF��CM=CG���Ƴ���MCH=��MCF+��FCH=45��=��HCG���õ���MCH�ա�GCH�����ǵõ�MH=GH�����ǵõ���HEG���ܳ�=GH+HE+GE=MH+HE+GE=FH+FM+HE+EH=FH+HE+EG+DG=EF+DE=2CD����A��AN��OB��N����CD��P����ON=$\frac{1}{2}$OB=6�����ݹ��ɶ����õ�AN=$\sqrt{A{O}^{2}-O{N}^{2}}=\sqrt{1{0}^{2}-{6}^{2}}$=8��ͨ����ACD�ס�AOB���б���ʽ������������
��� �⣺��1���ٵ���F��OB��ʱ��
����A��AH��OB��H����CD��G����ͼ1�٣�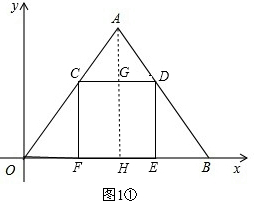
���С�AHE=90�㣮
���ı���CDEF�������Σ�
��CD=CF����DCF=��CFE=90�㣮
���AHE=��CFE=90�㣮
��CF��GH��
���AGC=��DCF=90�㣮
��AG��CD��
��CD��OB��CF��GH��
���ı���CGHF��ƽ���ı��Σ�
��CF=GH��
��AO=AB��AH��OB��
��OH=BH=$\frac{1}{2}$OB=6��
�ߡ�AHO=90�㣬OA=10��OH=6��
��AH=8��
��������CDEF�ı߳�Ϊx��
��GH=CF=CD=x��AG=AH-GH=8-x��
��CD��OB�����ACD�ס�AOB��
��AG��CD��AH��OB��
��$\frac{AG}{AH}$=$\frac{CD}{OB}$=$\frac{AC}{AO}$��
��$\frac{8-x}{8}$=$\frac{x}{12}$=$\frac{t}{10}$��
��ã�x=$\frac{24}{5}$��t=4��
��S=$\frac{576}{25}$��
�ڵ���F�ڡ�OAB�ڲ�ʱ��0��t��4����ͼ1�ڣ�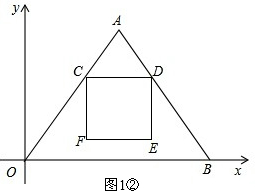
�ߡ�ACD�ס�AOB��
��$\frac{CD}{OB}$=$\frac{AC}{AO}$��
��$\frac{CD}{12}$=$\frac{t}{10}$��
��CD=$\frac{6t}{5}$��
��S=CD2=$\frac{36{t}^{2}}{25}$��
�۵���F�ڡ�OAB�ⲿʱ��4��t��10��
����A��AH��OB��H����ͼ1�ۣ�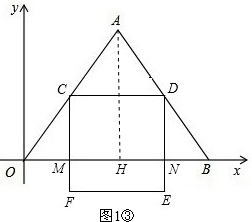
����CD=$\frac{6t}{5}$��OC=10-t��AH=8��CM��AH��
���OMC�ס�OHA��
��$\frac{CM}{AH}$=$\frac{OM}{OH}$=$\frac{OC}{OA}$��
��$\frac{CM}{8}$=$\frac{OM}{6}$=$\frac{10-t}{10}$��
��CM=8-$\frac{4t}{5}$��OM=6-$\frac{3t}{5}$��
��S=CD•CM=$\frac{6t}{5}$•��8-$\frac{4t}{5}$��=-$\frac{24}{25}$t2+$\frac{48}{5}$t��
������������0��t��4ʱ��S=$\frac{36{t}^{2}}{25}$����4��t��10ʱ��S=-$\frac{24}{25}$t2+$\frac{48}{5}$t��
��2������FO=FC����ͼ2�٣�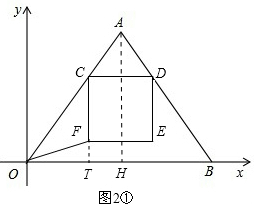
��ʱ��F�ڡ�OAB�ڲ���0��t��4��
����A��AH��OB��H���ӳ�CF��OB�ڵ�T��
�ɣ�1���ã�CF=CD=$\frac{6t}{5}$��CT=8-$\frac{4t}{5}$��OT=6-$\frac{3t}{5}$��
��FT=CT-CF=8-$\frac{4t}{5}$-$\frac{6t}{5}$=8-2t��
�ߡ�FTO=90�㣬��FT2+OT2=OF2��
�ࣨ8-2t��2+��6-$\frac{3t}{5}$��2=��$\frac{6t}{5}$��2��
�����ã�73t2-980t+2500=0��
��ã�t1=$\frac{250}{73}$��t2=10��
��0��t��4����t=$\frac{250}{73}$��
����CO=CF����ͼ2�ڣ�
��ʱ��F�ڡ�OAB�ⲿ��4��t��10��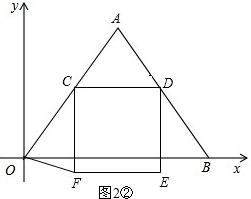
��CF=CD=$\frac{6t}{5}$��OC=10-t��CF=CO��
��$\frac{6t}{5}$=10-t��
��ã�t=$\frac{50}{11}$��
����OC=OF����ͼ2�ۣ�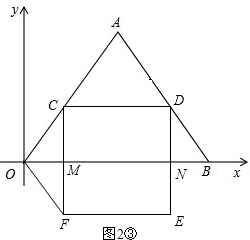
��ʱ��F�ڡ�OAB�ⲿ��4��t��10��
����CM=8-$\frac{4t}{5}$��CF=CD=$\frac{6t}{5}$��
��OC=OF��OM��CF��
��CM=FM=$\frac{1}{2}$CF��
��8-$\frac{4t}{5}$=$\frac{1}{2}$��$\frac{6t}{5}$��
��ã�t=$\frac{40}{7}$��
������������tΪ$\frac{250}{73}$���$\frac{50}{11}$���$\frac{40}{7}$��ʱ����OCFΪ���������Σ�
��3����EHG���ܳ��������仯��
��ͼ3����x���Ͻ�ȡFM=DG������CM��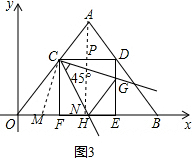
���ı���CDEF�������Σ���CD=CF����CDE=��CFE=��CFM=��FCD=90�㣬
��CD=CF���ڡ�CMF���CDG�У�$\left\{\begin{array}{l}{CF=CD}\\{��CFM=��CDG}\\{FM=DG}\end{array}\right.$��
���CFM�ա�CDG��
���DCG=��MCF��CM=CG��
�ߡ�HCG=45�㣬
���DCG+��FCH=45�㣬
���MCH=��MCF+��FCH=45��=��HCG��
�ڡ�MCH���GCH�У�$\left\{\begin{array}{l}{CM=CG}\\{��MCG=��GCH}\\{CH=CH}\end{array}\right.$��
���MCH�ա�GCH��
��MH=GH��
���HEG���ܳ�=GH+HE+GE=MH+HE+GE=FH+FM+HE+EH=FH+HE+EG+DG=EF+DE=2CD��
��A��AN��OB��N����CD��P����ON=$\frac{1}{2}$OB=6��
��AN=$\sqrt{A{O}^{2}-O{N}^{2}}=\sqrt{1{0}^{2}-{6}^{2}}$=8��
��CD��OB��
���ACD�ס�AOB��
��$\frac{CD}{OB}=\frac{AP}{AN}$����$\frac{CD}{12}=\frac{8-CD}{8}$��
��CD=$\frac{24}{5}$��
���EGH���ܳ�=2CD=$\frac{48}{5}$��
���� ���⿼�������������ε��ж������ʡ������ε����ʡ����������ε����ʡ�ƽ���ı��ε��ж������ʡ���һԪ���η��̡����ɶ�����֪ʶ����һ�����ۺ��ԣ��������ٽ�λ�ü������������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4cm | B�� | 6cm | C�� | 8cm | D�� | 9cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | -4 | C�� | -8 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
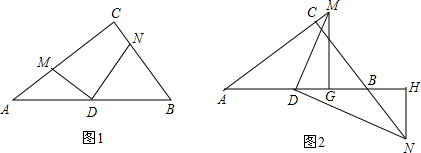
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com