
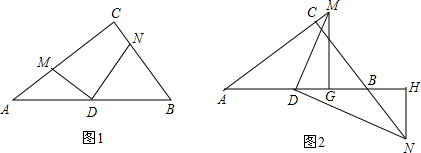
分析 (1)①分别过D作DP⊥BC于P,DQ⊥AC于Q,得到四边形DPCQ是矩形,求得∠QDP=90°,于是得到∠MDQ+∠QDN=∠QDN+∠NDP=90°,得到∠MDQ=∠NDP,证得△DMQ∽△DNP,得到$\frac{DM}{DN}=\frac{DQ}{DP}$,DQ=$\frac{1}{2}$BC,DP=$\frac{1}{2}$AC,于是得到结论;
②把已知数据代入比例式即可求得结果;
(2)DH⊥AB,如图2,过D作DQ⊥AC于Q.DP⊥BC于P,由(1)证得:$\frac{MD}{DN}=\frac{DQ}{DP}=\frac{BC}{AC}$,由于△AMG∽△ABC,于是得到$\frac{BC}{AC}=\frac{MG}{AG}=\frac{MG}{DH}$,等量代换得到$\frac{MD}{DN}=\frac{MG}{DH}$,推出△MDG∽△DNH,于是得到结论.
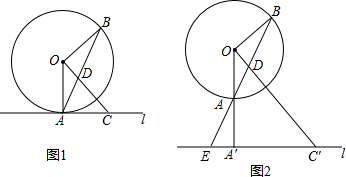
解答 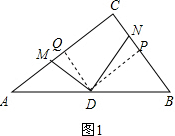 (1)证明:①分别过D作DP⊥BC于P,DQ⊥AC于Q,
(1)证明:①分别过D作DP⊥BC于P,DQ⊥AC于Q,
∴∠MQD=∠DNP=90°,
∵∠C=90°,
∴四边形DPCQ是矩形,
∴∠QDP=90°,
∵DM⊥DN,
∴∠MDQ+∠QDN=∠QDN+∠NDP=90°,
∴∠MDQ=∠NDP,
∴△DMQ∽△DNP,
∴$\frac{DM}{DN}=\frac{DQ}{DP}$,DQ=$\frac{1}{2}$BC,DP=$\frac{1}{2}$AC,
∴$\frac{DM}{DN}=\frac{BC}{AC}$;
②∵AQ=CQ=4,MQ=MC-CQ=5-4=1,
∵DQ=$\frac{1}{2}$BC=3,DP=$\frac{1}{2}$AC=4,
∵△DMQ∽△DNP,
∴$\frac{MD}{DN}=\frac{DQ}{DP}$,
∴NP=$\frac{4}{3}$,
∵CP=BP=3,
∴CN=3-$\frac{4}{3}$=$\frac{5}{3}$;
(2)DH⊥AB,
证明:如图2,过D作DQ⊥AC于Q.DP⊥BC于P,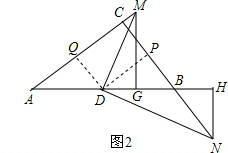 由(1)证得:$\frac{MD}{DN}=\frac{DQ}{DP}=\frac{BC}{AC}$,
由(1)证得:$\frac{MD}{DN}=\frac{DQ}{DP}=\frac{BC}{AC}$,
∵MG⊥AB于G,
∴∠ACB=∠AGM,∠A=∠A,
∴△AMG∽△ABC,
∴$\frac{BC}{AC}=\frac{MG}{AG}=\frac{MG}{DH}$,
∴$\frac{MD}{DN}=\frac{MG}{DH}$,
∵∠DMG=∠NDH,
∴△MDG∽△DNH,
∴∠DHN=∠MGD=90°,
即NH⊥AB.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,矩形的判定和性质,正确的作出辅助线构造相似三角形是解题的关键.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
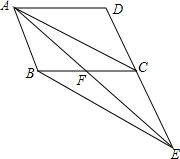 如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于F.
如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
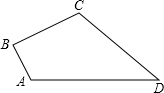 如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=1,BC=$\sqrt{2}$,CD=5,AD=2$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com