
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.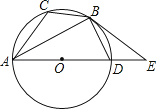
(1)求证:BE是⊙O的切线;
(2)若BC= ![]() ,AC=5,求圆的直径AD及切线BE的长.
,AC=5,求圆的直径AD及切线BE的长.
【答案】
(1)
证明:如图,
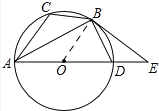
连接OB,∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是⊙O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在⊙O上,
∴BE是⊙O的切线,
(2)
解:如图2,
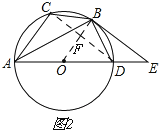
设圆的半径为R,连接CD,
∵AD为⊙O的直径,
∴∠ACCD=90°,
∵BC=BD,
∴OB⊥CD,
∴OB∥AC,
∵OA=OD,
∴OF= ![]() AC=
AC= ![]() ,
,
∵四边形ACBD是圆内接四边形,
∴∠BDE=∠ACB,
∵∠DBE=∠ACB,
∴△DBE∽△CAB,
∴ ![]() ,
,
∴ ![]() ,
,
∴DE= ![]() ,
,
∵∠OBE=∠OFD=90°,
∴DF∥BE,
∴ ![]() ,
,
∴ 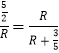 ,
,
∵R>0,
∴R=3,
∵BE是⊙O的切线,
∴BE= ![]() =
= ![]() =
= ![]()
【解析】(1)先根据等弦所对的劣弧相等,再结合∠EBD=∠CAB从而得到∠BAD=∠EBD,最后用直径所对的圆周角为直角即可;(2)利用三角形的中位线先求出OF,再用平行线分线段成比例定理求出半径R,最后用切割线定理即可.此题是切线的判定,主要考查了圆周角的性质,切线的判定,平行线分线段成比例定理,相似三角形的判定和相似,圆内接四边形的性质,解本题的关键是作出辅助线.


科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
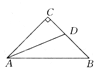
【题目】如图所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,能否在AB上确定一点E,使△BDE的周长等于AB的长?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( ) 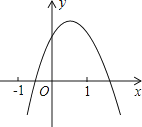
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.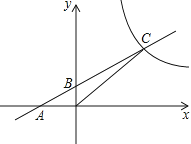
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
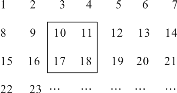
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( ) 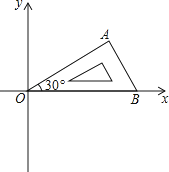
A.( ![]() ,﹣1)
,﹣1)
B.(1,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市文化底蕴深厚,旅游资源丰富,古隆中、习家池、鹿门寺三个景区是人们节假日玩的热点景区,张老师对八(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别:A、游三个景区;B、游两个景区;C、游一个景区;D、不到这三个景区游玩.现根据调查结果绘制了不完整的条形统计图和扇形统计图,请结合图中信息解答下列问题: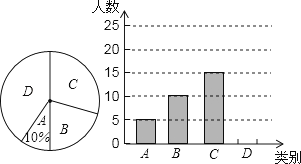
(1)八(1)班共有学生人,在扇形统计图中,表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若张华、李刚两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,则他们同时选中古隆中的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com