
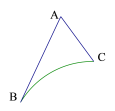
【题目】如图所示,AB=6,AC=3,∠BAC=60°,![]() 为⊙O上的一段弧,且∠BOC=60°,分别在
为⊙O上的一段弧,且∠BOC=60°,分别在![]() 、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
【答案】![]()
【解析】
连接AP、O、OA,分别以AB、AC所在直线为对称轴,作出P关于AB的对称点M,P关于AC的对称点N,连接MN,交AB于点E,交AC于点F,连接PE、PF,所以
AM=AP=AN,设AP=r,则MN=![]() ,所以PE+EF+PF=ME+EF+FN=MN=
,所以PE+EF+PF=ME+EF+FN=MN=![]() ,即当AP最小时,PE+EF+PF可取最小值,由AP+OP≥OA可知AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,利用勾股定理即可求得AP的长度,即可解答.
,即当AP最小时,PE+EF+PF可取最小值,由AP+OP≥OA可知AP≥OA﹣OP,即点P在OA上时,AP可取得最小值,利用勾股定理即可求得AP的长度,即可解答.
连接BC,取AB的中点D,连接CD,如图1

则AD=BD=3
∴AD=BD=AC
∵∠BOC=60°
∴△ADC是等边三角形
∴CD=AC=3
∴CD=![]() AB
AB
∴∠ACB=90°
连接AP、O、OA,分别以AB、AC所在直线为对称轴,作出P关于AB的对称点M,P关于AC的对称点N,连接MN,交AB于点E,交AC于点F,连接PE、PF,

∴AM=AP=AN
∵∠MAB=∠PAB,∠NAC=∠PAC
∵∠BAC=∠PAB+∠PAC=∠MAB+∠NAC=60°
∴∠MAN=120°
∴M、P、N在以A为圆心AP为半径的圆上
设AP=r,则MN=![]()
∵PE=ME,PF=FN
∴PE+EF+PF=ME+EF+FN=MN=![]()
∴当AP最小时,PE+EF+PF可取最小值
∵AP+OP≥OA
∴AP≥OA﹣OP,即点P在OA上时,AP可取得最小值
在Rt△ABC中,∵AB=6,AC=3,∠BAC=60°
∴BC=![]()
∵∠BOC=60°,OB=OC
∴△OBC是等边三角形
∴OC=BC=![]() ,作OH⊥AC交AC的延长线于H
,作OH⊥AC交AC的延长线于H
在Rt△OCH中,∵OC=![]() ,∠OCH=30°
,∠OCH=30°
∴OH=![]() OC=
OC=![]() ,CH=
,CH=![]() OH=
OH=![]()
在Rt△AOH中,AO=![]()
此时AP=r=![]()
∴PE+EF+PF的最小值为![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】请你利用直角坐标平面上任意两点(x1,y1)、(x2,y2)间的距离公式![]() 解答下列问题:
解答下列问题:
已知:反比例函数![]() 与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数
与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数![]() 图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)x4﹣5x2+4=0是一个一元四次方程.
(探索)根据该方程的特点,通常用“换元法”解方程:
设x2=y,那么x4= ,于是原方程可变为 .
解得:y1=1,y2= .
当y=1时,x2=1,∴x=±1;
当y= 时,x2= ,∴x= ;
原方程有4个根,分别是 .
(应用)仿照上面的解题过程,求解方程:(x2﹣2x)2+(x2﹣2x)﹣6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=2x2+bx+c.当x=1时,y=4;当x=﹣2,y=﹣5.
(1)求y关于x的二次函数的解析式;
(2)在直角坐标系中把(1)中的图象抛物线平移到顶点与原点重合,应该怎样平移?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=a与抛物线![]() 交于A、B两点(A在B的左侧),交y轴于点C
交于A、B两点(A在B的左侧),交y轴于点C
(1)若AB=4,求a的值
(2)若抛物线上存在点D(不与A、B重合),使![]() ,求a的取值范围
,求a的取值范围
(3)如图2,直线y=kx+2与抛物线交于点E、F,点P是抛物线上的动点,延长PE、PF分别交直线y=-2于M、N两点,MN交y轴于Q点,求QM·QN的值。
图1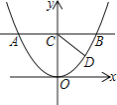 图2
图2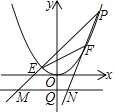
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
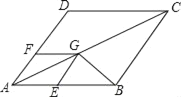
【题目】如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com