
【题目】(发现)x4﹣5x2+4=0是一个一元四次方程.
(探索)根据该方程的特点,通常用“换元法”解方程:
设x2=y,那么x4= ,于是原方程可变为 .
解得:y1=1,y2= .
当y=1时,x2=1,∴x=±1;
当y= 时,x2= ,∴x= ;
原方程有4个根,分别是 .
(应用)仿照上面的解题过程,求解方程:(x2﹣2x)2+(x2﹣2x)﹣6=0
【答案】:(探索)y2,y2﹣5y+4=0,4,4,4,±2,±1,±2;(应用)x=1±![]() .
.
【解析】
(探索)利用换元的思想求出所求方程的解即可.
(应用)利用换元的思想求出所求方程的解即可.
解:(探索)设x2=y,那么x4=y2,于是原方程可变为y2﹣5y+4=0.
解得:y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
原方程有4个根,分别是±1,±2.
故答案为:y2,y2﹣5y+4=0,4,4,4,±2,±1,±2,
(应用)(x22x)2+(x22x)6=0,
设y=x22x,方程变形得:y2+y6=0,
解得:y=2或y=3,
可得x22x=2或x22x=3(无解),
解得:x=1±![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为________.
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为________.
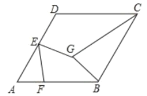
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店销售儿童书刊,一天可出售20套,每套盈利40元.为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多出售2套.设每套降价x元,书店一天可获利润y元.
(1)求y关于x的函数解析式.
(2)若要书店每天盈利1200元,则需降价多少元?
(3)当每套书降价多少元时,书店可获最大利润?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+4交x轴于A,B两点,顶点是C.
(1)求△ABC的面积;
(2)若点P在抛物线y=-x2+4上, 且S△PAB=![]() S△ABC,求点P的坐标。
S△ABC,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC的顶点A(-8,0)、C(0,6),点D是BC边上的中点,抛物线y=ax2+bx经过A、D两点,如图所示.
(1)求点D关于y轴的对称点D′的坐标及a、b的值;
(2)在y轴上取一点P,使PA+PD长度最短,求点P的坐标;
(3)将抛物线y=ax2+bx向下平移,记平移后点A的对应点为A1,点D的对应点为D1,当抛物线平移到某个位置时,恰好使得点O是y轴上到A1、D1两点距离之和OA1+OD1最短的一点,求此抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,点A(a,0),B(m,n),C(p,n),其中m>p>0,n>0,点A,C在直线y=﹣2x+10上,AC=2![]() ,OB平分∠AOC.
,OB平分∠AOC.
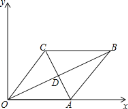
(1)求△OAC的面积;
(2)求证:四边形OABC是菱形;
(3)射线OB上是否存在点P,使得△PAC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com