【题目】某书店销售儿童书刊,一天可出售20套,每套盈利40元.为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多出售2套.设每套降价x元,书店一天可获利润y元.
(1)求y关于x的函数解析式.
(2)若要书店每天盈利1200元,则需降价多少元?
(3)当每套书降价多少元时,书店可获最大利润?最大利润为多少?
【答案】(1)
；(2)降价20元；(3)x=15时，y取最大值1250.
【解析】
（1）根据题意设出每天降价x元以后，准确表示出每天书刊的销售量，列出利润y关于降价x的函数关系式；
（2）根据题意列出关于x的一元二次方程，通过解方程即可解决问题；
（3）运用函数的性质即可解决．
解：（1）设每套书降价x元时，所获利润为y元，
则每天可出售20+4×
=20+2x套；
由题意得：y=（40-x）（20+2x）
=-2x2+80x-20x+800
=-2x2+60x+800；
（2）∵y=-2x2+60x+800=-2（x-15）2+1250
当y=1200时，-2（x-15）2+1250=1200，
整理得：（x-15）2=25，
解得x=10或20但为了尽快减少库存，所以只取x=20，
答：若每天盈利1200元，为了尽快减少库存，则应降价20元；
（3）∵y=-2（x-15）2+1250=1200
则当x=15时，y取得最大值1250；
即当将价15元时，该书店可获得最大利润1250元．
寒假学与练系列答案科目：初中数学 来源： 题型：
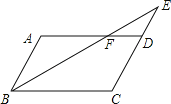
【题目】如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，CD=2DE．若△DEF的面积为a，则平行四边形ABCD的面积为 ▲ （用a的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠ACB=90°，CE是中线，△ACD与△ACE关于直线AC对称．
（1）求证：四边形ADCE是菱形；
（2）求证：BC=ED．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC的延长线于点F，以EC、CF为邻边作ECFG.
(1)如图1，证明ECFG为菱形；
(2)如图2,若∠ABC=120°,连接BG、CG,并求出∠BDG的度数：
(3)如图3,若∠ABC=90°，AB=6,AD=8,M是EF的中点，求DM的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】人民商场销售某种商品，统计发现：每件盈利
元时，平均每天可销售
件．经调查发现，该商品每降价
元，商场平均每天可多售出
件．
假如现在库存量太大，部门经理想尽快减少库存，又想销售该商品日盈利达到
元，请你帮忙思考，该降价多少？
假如部门经理想销售该商品的日盈利达到最大，请你帮忙思考，又该如何降价？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用适当的方法解方程。
（1）4(x-3) 
=36
（2）x2-4x＋1＝0.
（3）
-7x+6=0
（4）
（5）(y－1)2＋2y(1－y)＝0.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（发现）x4﹣5x2+4＝0是一个一元四次方程．
（探索）根据该方程的特点，通常用“换元法”解方程：
设x2＝y，那么x4＝ ，于是原方程可变为 ．
解得：y1＝1，y2＝ ．
当y＝1时，x2＝1，∴x＝±1；
当y＝ 时，x2＝ ，∴x＝ ；
原方程有4个根，分别是 ．
（应用）仿照上面的解题过程，求解方程：（x2﹣2x）2+（x2﹣2x）﹣6＝0
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一元二次方程ax2+bx+c=0（a≠0）中，下列说法：
①若a+b+c=0，则b2﹣4ac＞0；
②若方程两根为﹣1和2，则2a+c=0；
③若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；
④若b=2a+c，则方程有两个不相等的实根．其中正确的有（ ）
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2016年，某贫困户的家庭年人均纯收入为2500元，通过政府产业扶持，发展了养殖业后，到2018年，家庭年人均纯收入达到了3600元．
（1）求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率；
（2）若年平均增长率保持不变，2019年该贫困户的家庭年人均纯收入是否能达到4200元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com