
【题目】如图1,已知直线y=a与抛物线![]() 交于A、B两点(A在B的左侧),交y轴于点C
交于A、B两点(A在B的左侧),交y轴于点C
(1)若AB=4,求a的值
(2)若抛物线上存在点D(不与A、B重合),使![]() ,求a的取值范围
,求a的取值范围
(3)如图2,直线y=kx+2与抛物线交于点E、F,点P是抛物线上的动点,延长PE、PF分别交直线y=-2于M、N两点,MN交y轴于Q点,求QM·QN的值。
图1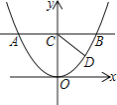 图2
图2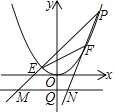
【答案】(1)![]() ;(2)
;(2)![]() ;(3)8
;(3)8
【解析】
(1)将两个函数解析式联立,解一元二次方程求得A、B的横坐标,进而表示出AB,即可解答;
(2)由(1)可得CD=![]() AB=
AB=![]() ,设D
,设D![]() ,过点D作DH⊥y轴于点H,利用勾股定理可知
,过点D作DH⊥y轴于点H,利用勾股定理可知![]() ,进而得到
,进而得到![]() ,得到
,得到![]() ,根据函数图象可知
,根据函数图象可知![]() ,即可求得a的取值范围;
,即可求得a的取值范围;
(3)设E(![]() ),F(
),F(![]() ),P(
),P(![]() ),分别表示EP和FP的解析式,当
),分别表示EP和FP的解析式,当![]() 时,求得
时,求得![]() ,
,![]() ,联立
,联立![]() 和y=kx+2,得到
和y=kx+2,得到![]() ,利用一元二次方程根与系数的关系得到
,利用一元二次方程根与系数的关系得到![]() ,代入
,代入![]() 即可解答.
即可解答.
(1)联立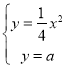 ,
,
∴![]() ,解得:
,解得:![]()
∴![]()
∴![]()
(2)由(1)知AB=![]() ,
,
∴CD=![]() AB=
AB=![]()
设D![]()

过点D作DH⊥y轴于点H,则![]()
∴![]()
∴![]()
又![]()
∴![]()
∴![]()
又![]()
∴![]()
∴![]()
(3)设E(![]() ),F(
),F(![]() ),P(
),P(![]() )
)
EP解析式为![]()
将P,E代入可得:![]()
当![]() 时,可求
时,可求![]() ,
,
同理可求FP的解析式为![]()
![]()
又联立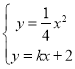 得:
得:![]()
∴![]()
∴![]()
![]()


科目:初中数学 来源: 题型:
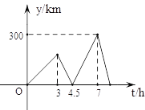
【题目】在一条笔直的公路上有A、B两地,甲、乙两辆货车都要从A地送货到B地,甲车先从A地出发匀速行驶,3小时后,乙车从A地出发,并沿同一路线匀速行驶,当乙车到达B地后立刻按原速返回,在返回途中第二次与甲车相遇。甲车出发的时间记为t (小时),两车之间的距离记为y(千米),y与t的函数关系如图所示,则乙车第二次与甲车相遇时,甲车距离A地___千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
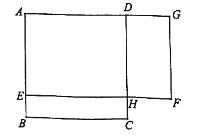
【题目】如图, ![]() 是一块边长为4米的正方形苗圃,园林部门将其改造为矩形
是一块边长为4米的正方形苗圃,园林部门将其改造为矩形![]() 的形状,其中点
的形状,其中点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上,
的延长线上, ![]() 设
设![]() 的长为
的长为![]() 米,改造后苗圃
米,改造后苗圃![]() 的面积为
的面积为![]() 平方米.
平方米.
(1) ![]() 与
与![]() 之间的函数关系式为 (不需写自变量的取值范围);
之间的函数关系式为 (不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃![]() 的面积与原正方形苗圃
的面积与原正方形苗圃![]() 的面积相等,请问此时
的面积相等,请问此时![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
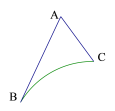
【题目】如图所示,AB=6,AC=3,∠BAC=60°,![]() 为⊙O上的一段弧,且∠BOC=60°,分别在
为⊙O上的一段弧,且∠BOC=60°,分别在![]() 、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
、线段AB和AC上选取点P、E、F,则PE+EF+FP的最小值为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
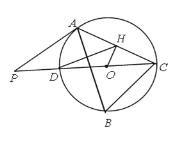
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示。
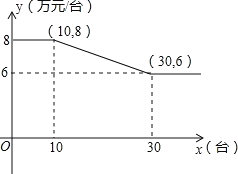
(1)当x=10时,公司销售机器人的总利润为___万元;
(2)当10x30时,求出y与x的函数关系式;
(3)问:销售量为多少台时,公司销售机器人的总利润为37.5万元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com