
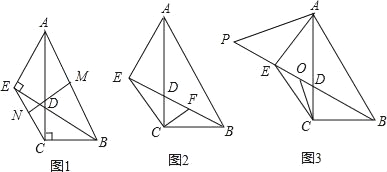
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=2BC,点D在边AC上,连接BD,过A作BD的垂线交BD的延长线于点E.
(1)若M,N分别为线段AB,EC的中点,如图1,求证:MN⊥EC;
(2)如图2,过点C作CF⊥EC交BD于点F,求证:AE=2BF;
(3)如图3,以AE为一边作一个角等于∠BAC,这个角的另一边与BE的延长线交于P点,O为BP的中点,连接OC,求证:OC=![]() (BE﹣PE).
(BE﹣PE).
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)连接EM、CM,直角三角形斜边上的中线等于斜边的一半得EM=CM;再由等腰三角形三线合一的性质得出结论;
(2)证明△AEC∽△BFC,得![]() 由AC=2BC得AE=2BF;
由AC=2BC得AE=2BF;
(3)证明△ACB∽△AEP,得![]() 从而知道AE=2PE,由AE=2BF得PE=BF;根据直角三角形斜边中线等于斜边一半得OC=
从而知道AE=2PE,由AE=2BF得PE=BF;根据直角三角形斜边中线等于斜边一半得OC=![]() EF,代入得结论.
EF,代入得结论.
证明:(1)如图1,连接EM、CM,
∵AE⊥BE,M是AB的中点,
∴EM=![]() AB,CM=
AB,CM=![]() AB,
AB,
∴EM=CM,
∵N是EC的中点,
∴MN⊥EC;
(2)如图2,∵∠ECF=90°,∠ACB=90°,
∴∠ECA+∠ACF=90°,∠ACF+∠FCB=90°,
∴∠ECA=∠FCB,
∵∠CFB=∠ECF+∠CEF=90°+∠CEF,
∠AEC=∠AEB+∠CEF=90°+∠CEF,
∴∠CFB=∠AEC,
∴△AEC∽△BFC,
∴![]()
∵AC=2BC,
∴AE=2BF;
(3)如图3,过点C作CF⊥EC交BD于点F,
∵∠AEP=∠ACB=90°,∠BAC=∠PAE,
∴△ACB∽△AEP,
∴![]()
∵AC=2BC,
∴AE=2PE,
∵AE=2BF,
∴PE=BF,
∵O为BP的中点,
∴PO=BO,
∴EO=FO,
∴CO=![]() EF=
EF=![]() (BE﹣BF)=
(BE﹣BF)=![]() (BE﹣PE).
(BE﹣PE).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象
如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度; ②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km; ④甲比乙先到达终点.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
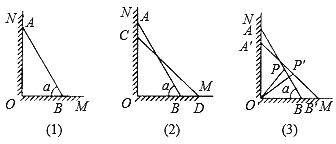
【题目】如图(1)所示,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面所成的角为60度.
(1)求图(1)中的AO与BO的长度;
(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图(2)所示,设A点下滑到C点,B点向右滑行到D点,并且AC:BD2:3,请计算AC的长度;
②如图(3)所示,当A点下滑到A点,B点向右滑行到B点时,梯子AB的中点P也随之运动到P点,若POP15,试求AA的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CDOE;
(3)若![]() ,求OE的长.
,求OE的长.
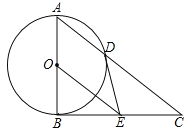
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个题目:
按照给定的计算程序,确定使代数式n(n+2)大于2000的n的最小正整数值.想一想,怎样迅速找到这个n值,请与同学们交流你的体会.
小亮尝试计算了几组n和n(n+2)的对应值如下表:
n | 50 | 40 | |
n(n+2) | 2600 | 1680 |
(1)请你继续小亮的尝试,再算几组填在上表中(几组随意,自己画格),并写出满足题目要求的n的值;
(2)结合上述过程,对于“怎样迅速找到n值”这个问题,说说你的想法.
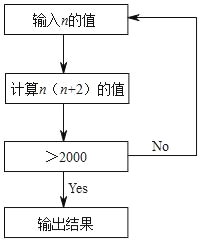
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 与
与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与反比例函数
两点,与反比例函数![]() 相交于
相交于![]() 两点,分别过
两点,分别过![]() 两点作
两点作![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() ,有下列四个结论:①
,有下列四个结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() ∽
∽![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
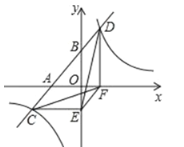
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个黑布袋,A布袋中有四个除标号外完全相同的小球,小球上分别标有数字0,1,2,3,B布袋中有三个除标号外完全相同的小球,小球上分别标有数字0,1,2.小明先从A布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从B布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)用(m,n)表示小明取球时m与n的对应值,画出树状图(或列表),写出(m,n)的所有取值;
(2)求关于x的一元二次方程![]() 没有实数根的概率.
没有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=n与二次函数y=![]() (x﹣2)2﹣1的图象交于点B,点C,二次函数图象的顶点为A,当△ABC是等腰直角三角形时,则n的值为( )
(x﹣2)2﹣1的图象交于点B,点C,二次函数图象的顶点为A,当△ABC是等腰直角三角形时,则n的值为( )
A. 1B. ![]() C. 2﹣
C. 2﹣![]() D. 2+
D. 2+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com