
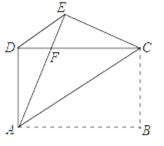
【题目】如图,在长方形ABCD中,AB>BC,把长方形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE
求证:(1)△AED≌△CDE
(2)△EFD是等腰三角形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据矩形的性质可得出AD=BC、AB=CD,结合折叠的性质可得出AD=CE、AE=CD,进而即可证出△ADE≌△CED(SSS);
(2)根据全等三角形的性质可得出∠DEF=∠EDF,利用等边对等角可得出EF=DF,由此即可证出△DEF是等腰三角形.
证明:(1)∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
由折叠的性质可得:BC=CE,AB=AE,
∴AD=CE,AE=CD.
在△ADE和△CED中,
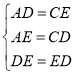 ,
,
∴△ADE≌△CED(SSS).
(2)由(1)得△ADE≌△CED,
∴∠DEA=∠EDC,即∠DEF=∠EDF,
∴EF=DF,
∴△DEF是等腰三角形.


科目:初中数学 来源: 题型:
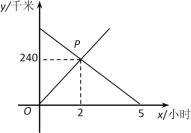
【题目】甲、乙二人驾车分别从A,B两地同时出发,相向而行.下图是二人离A地的距离y(千米)与所用时间x(小时)的关系.
(1)请说明交点P所表示的实际意义: ;
(2)试求出A,B两地之间的距离;
(3)甲从A地到达B地所需的时间为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年11月2日﹣4日,江西省中小学生研学实践教育推进会和全国中小学综合实践活动(研学实践教育)论坛相继在抚州举行.为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,抚州市某中学决定组织部分班级去仙盖山开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.参加此次研学旅行活动的老师和学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
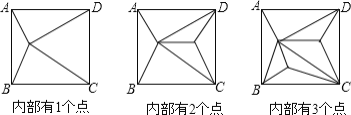
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是矩形,已知PB=PC.
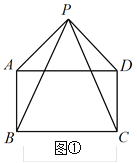
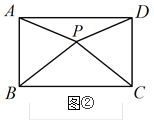
(1)若P是矩形外一点,求证:PA=PD;
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC与三角形![]() 在平面直角坐标系中的位置如图所示,三角形
在平面直角坐标系中的位置如图所示,三角形![]() 是由三角形ABC经过平移得到的.
是由三角形ABC经过平移得到的.
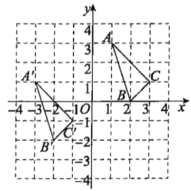
(1)分别写出点![]()
![]()
![]() 的坐标;
的坐标;
(2)说明三角形![]() 是由三角形ABC经过怎样的平移得到的;
是由三角形ABC经过怎样的平移得到的;
(3)若点![]() 是三角形ABC内的一点,则平移后点P在三角形
是三角形ABC内的一点,则平移后点P在三角形![]() 内的对应点为P‘,写出点P’的坐标.
内的对应点为P‘,写出点P’的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AC平分∠BAD,CE⊥AB于E,CD⊥AD于F,且BC=DC.
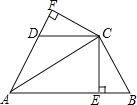
(1)BE与DF是否相等?请说明理由;
(2)若DF=1,AD=3,求AB的长;
(3)若△ABC的面积是23,△ADC面积是18,直接写出△BEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
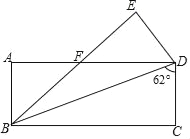
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com