
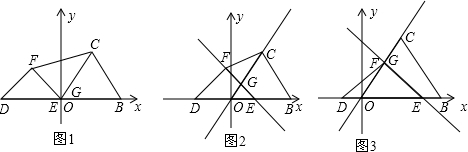
分析 (1)①把t=1代入求解即可,
②由等腰直角三角形及等边三角形的性质得出∠DEF=45°,∠COB=60°,再利用∠FGC=∠OGE=180°-45°-60°求解即可.
③过点G作GH⊥OE于点H,先求出GH,利用OH+HE=OH+$\sqrt{3}$OH=1+$\sqrt{3}$,得出OH=1,即可得出G点坐标
(2)①过点G作GP⊥OB于点P,设OP=a,由特殊三角形性质得出GP=$\sqrt{3}$a=PE=DP,利用DE=DP+PE=2$\sqrt{3}$a=6,得a=$\sqrt{3}$,利用OE=OP+PE=(1+$\sqrt{3}$)a,即可得出t的值;
②分三种情况当0<t<$\sqrt{3}$时,当$\sqrt{3}$<t<3时,当t>3时,分别求解即可.
解答 解:(1)①∵△DEF沿X轴的正方向以每秒$\sqrt{3}$+1个单位运动,
∴OE=$\sqrt{3}$+1,
②∵在等腰直角△DEF中,∠DEF=45°,在等边△BOC中,∠COB=60°,
∴∠FGC=∠OGE=180°-45°-60°=75°.
③如图2,过点G作GH⊥OE于点H,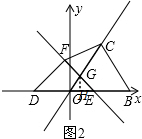
∵∠COB=60°,
∴GH=$\sqrt{3}$OH=HE,
∴OH+HE=OH+$\sqrt{3}$OH=1+$\sqrt{3}$,即OH=1,
∴G(1,$\sqrt{3}$).
(2)①如图3,过点G作GP⊥OB于点P,设OP=a,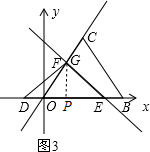
∴GP=$\sqrt{3}$a=PE=DP,
∴DE=DP+PE=2$\sqrt{3}$a=6,得a=$\sqrt{3}$,
∴OE=OP+PE=(1+$\sqrt{3}$)a,即t=$\frac{(1+\sqrt{3})a}{1+\sqrt{3}}$=a=$\sqrt{3}$,
②当0<t<$\sqrt{3}$时,如图4,过点F,C作GM⊥DE,CN⊥OB,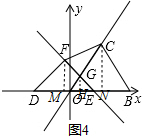
OH=t,HG=$\sqrt{3}$t=EH,
∴HM=3-$\sqrt{3}$t,HN=3-t,MH=6,FM=3,CN=3$\sqrt{3}$,
则S△FCG=S梯形MNCF-S梯形GHMF-S梯形GHNC=$\frac{3+\sqrt{3}}{2}$t2-(6+3$\sqrt{3}$)t+$\frac{9\sqrt{3}+9}{2}$(0<t<$\sqrt{3}$),
同理,当$\sqrt{3}$<t<3时,S△FCG=-$\frac{3+\sqrt{3}}{2}$t2+(6+3$\sqrt{3}$)t-$\frac{9\sqrt{3}+9}{2}$,
当t>3时,S△FCG=$\frac{3+\sqrt{3}}{2}$t2-(6+3$\sqrt{3}$)t+$\frac{9\sqrt{3}+9}{2}$.
点评 本题主要考查了特殊三角形及梯形的综合运用,解题的关键是能结合图形,分三种情况讨论求解.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -$\frac{3}{2}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
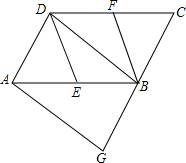 如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.
如图,在?ABCD中,E,F分别是边AB,CD的中点,BD是对角线,AG∥BD交GB的延长线于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com