
【题目】如图,在Rt△OAB中,∠A=90°,OA=4,AB=3,动点M从点A出发,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒![]() 个单位长度的速度,沿OB向终点B移动.设运动时间为t秒.
个单位长度的速度,沿OB向终点B移动.设运动时间为t秒.
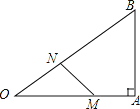
(1)用含t的代数式表示点N到OA的距离;
(2)设△OMN的面积是S,求S与t之间的函数表达式;当t为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
【答案】(1点N到OA的距离为![]() ;(2)S=-
;(2)S=-![]() ,当t=2时,S有最大值,最大值为S=
,当t=2时,S有最大值,最大值为S=![]() .(3) t=2或t=
.(3) t=2或t=![]() 时,△OMN是直角三角形
时,△OMN是直角三角形
【解析】
试题分析:(1)由勾股定理计算出OB,再用三角函数即可;
(2)得到S与t的函数关系,从而确定出面积最大值;
(3)要使△OMN是直角三角形,一个直角三角形和它相似,即可;
试题解析:(1)在Rt△OAB中,OB=![]() =5,
=5,
∴点N到OA的距离为ON×sin∠O=![]() ;
;
(2)S=![]() (4-t)×
(4-t)×![]() =-
=-![]() ,
,
当t=-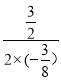 =2时,S有最大值,
=2时,S有最大值,
最大值为S=-![]() ×22+
×22+![]() ×2=
×2=![]() .
.
(3)∵△ABO为直角三角形,
∴以M、N、O为顶点的三角形和△ABO相似;
当△OMN∽△OAB时,
∴![]() ,
,
∴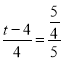 ,
,
∴t=2,
当△OMN∽△OBA时,
∴![]() ,
,
∴ ,
,
∴t=![]() ,
,
∴t=2或t=![]() 时,△OMN是直角三角形
时,△OMN是直角三角形


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】中秋节当天,小明将收到的一条短信,发送给若干人,每个收到短信的人又给相同数量的人转发了这条短信,此时包括小明在内收到这条短信的人共有111人,问小明给( )人发了短信?
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知互不平行的两条线段AB,CD关于直线l对称,AB,CD所在直线交于点P,下列结论中:①AB=CD;②点P在直线l上; ③若A、C是对称点,则l垂直平分线段AC; ④若B、D是对称点,则PB=PD.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD,AD=BC
B.∠A=∠B,∠C=∠D
C.AB∥CD,∠C=∠A
D.AB=AD,CB=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com