
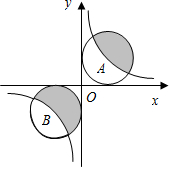
 如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π.
如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,则图中阴影部分的面积等于3π. 分析 由反比例函数的对称性结合切线的性质即可得出:⊙A和⊙B半径相同,且两圆关于原点O中心对称,由此即可得出图中阴影部分的面积等于⊙A的面积,设⊙A的半径为r,则点A的坐标为(r,r),根据反比例函数系数k的几何意义即可得出r2=3,再根据圆的面积公式即可得出图中阴影部分的面积.
解答 解:∵⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数y=$\frac{3}{x}$的图象上,
∴⊙A和⊙B半径相同,且两圆关于原点O中心对称,
∴图中阴影部分的面积等于⊙A的面积.
设⊙A的半径为r,则点A的坐标为(r,r),
∵圆心A在反比例函数y=$\frac{3}{x}$的图象上,
∴r2=3,
∴S阴影=πr2=3π.
故答案为:3π.
点评 本题考查了反比例函数系数k的几何意义、反比例函数的性质、切线的性质以及圆的面积,根据反比例函数的对称性找出图中阴影部分的面积等于⊙A的面积是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.
如图,Rt△ABC,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-y=300}\\{(1+20%)x-(1-10%)y=980}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=300}\\{(1-20%)x-(1+10%)y=980}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y=300}\\{20%x-10%y=980}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=300}\\{(1-20%)x-(1-10%)y=980}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,甲、乙两人沿着边长为8米的正方形的边按逆时针方向行走;甲从点A出发以1m/s的速度行走,同时乙从点B出发以1.4m/s的速度行走,则当乙第一次追上甲时,将在正方形的( )
如图所示,甲、乙两人沿着边长为8米的正方形的边按逆时针方向行走;甲从点A出发以1m/s的速度行走,同时乙从点B出发以1.4m/s的速度行走,则当乙第一次追上甲时,将在正方形的( )| A. | AB边上 | B. | BC边长 | C. | CD边上 | D. | DA边上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 抛一枚硬币,正面朝上 | |
| C. | 某运动员射击一次,击中靶心 | |
| D. | 明天一定是晴天 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com