
【题目】(1)感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知DB,DC数量关系为: .
(2)探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,(1)中的结论是否成立?请作出判断并给予证明.
(3)应用:如图3,在四边形ABCD中,DB=DC,∠ABD+∠ACD=180°,∠ABD<90°,DE⊥AB于点E,试判断AB,AC,BE的数量关系,并说明理由.

【答案】(1)BD=CD;(2)成立,证明详见解析;(3)AB=AC+2BE,证明详见解析.
【解析】
(1)结论:BD=CD.只要证明△ADC≌△ADB即可;
(2)结论成立.如图②中,作DE⊥AB于E,DF⊥AC于F,只要证明△ADC≌△ADB即可;
(3)如图③中,连接AD.作DF⊥AC于F.首先证明△DFC≌△DEB(AAS),再证明Rt△ADF≌Rt△ADE(HL)即可解决问题.
解:(1)结论:DB=DC.
理由:∵∠B+∠C=180°,∠B=90°,
∴∠B=∠C=90°,
∵∠DAC=∠DAB,AD=AD,
∴△ADC≌△ADB.
∴BD=CD.
故答案为BD=CD.
(2)结论成立.
理由:如图②中,作DE⊥AB于E,DF⊥AC于F.

∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△EDB中,
 ,
,
∴△DFC≌△DEB,
∴DC=DB.
(3)结论:AB=AC+2BE.
理由:如图③中,连接AD.作DF⊥AC于F.

∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
 ,
,
∴△DFC≌△DEB(AAS),
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
![]() ,
,
∴Rt△ADF≌Rt△ADE(HL),
∴AF=AE,
∴AB=AE+BE=AC+CF+BE=AC+2BE.


科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形于1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示三角形的两条直角边(x>y),下列四个说法:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 。其中说法正确的是( )
。其中说法正确的是( )

A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD//BC,∠A=90°,E为AB上一点,且AE=BC,∠1=∠2.
请说明:(1)△ADE与△BEC全等吗?请说明理由;
(2)判断△CDE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
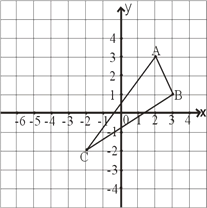
【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
(1)请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直写出D、E、F的坐标.D、E、F点的坐标是:D( , ) E( , ) F( , );
(2)求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形与中间的小正方形拼成的一个大正方形如果大正方形的面积是13,小正方形的面积是4,直角三角形的较短直角边为a,较长直角边为b,那么![]() 的值为______________.
的值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
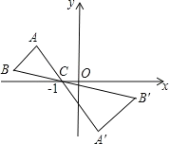
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把长与宽之比为![]() 的矩形纸片称为标准纸.不难发现,将一张标准纸如图一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸
的矩形纸片称为标准纸.不难发现,将一张标准纸如图一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸![]() ,
,![]() ,
,![]() ,那么把它第
,那么把它第![]() 次对开后所得标准纸的周长是________.
次对开后所得标准纸的周长是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com