
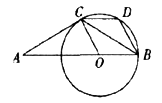

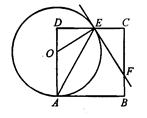
 ∴弧BC的弧长=
∴弧BC的弧长= 然后根据圆锥的计算求圆锥的底面圆半径.
然后根据圆锥的计算求圆锥的底面圆半径. ,∠ACB=120°,∴∠ABC=∠A=30°。
,∠ACB=120°,∴∠ABC=∠A=30°。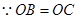 ,∠CBO=∠BCO=30°,
,∠CBO=∠BCO=30°, ,
,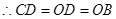 ,
,
 ACtan∠A=6tan30°=
ACtan∠A=6tan30°= ,
,



科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 名称 | 四等分圆的面积 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
| 选用的工具 | 带刻度的三角板 | 量角器 | 带刻度的三角板、圆规 |
| 画出示意图 |  | | |
| 简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. | | |
| 指出对称性 | 既是轴对称图形又是中心对称图形 | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
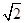 ,AC=3
,AC=3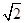 ,BC=6,则⊙O的半径是
,BC=6,则⊙O的半径是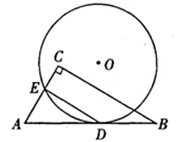
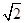 C.2
C.2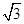 D.
D.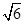
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com