
【题目】某电脑公司经销甲种型号电脑,受各方因素影响,电脑价格将不断下降,今年三月份的电脑售价比去年同期每台降价900元,如果卖出相同数量的电脑,去年销售为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3400元,乙种电脑每台进价为3000元,公司预计用不多于4.8万元且不少于4.7万元的资金购进这两种电脑共15台,则共有几种进货方案?
【答案】(1)今年三月份甲种电脑每台售价为3600元;(2)该公司共有三种进货方案,方案1:购进5台甲种电脑,10台乙种电脑;方案2:购进6台甲种电脑,9台乙种电脑;方案3:购进7台甲种电脑,8台乙种电脑.
【解析】
(1)设今年三月份甲种电脑每台售价为x元,则去年同期甲种电脑每台售价为(x+900)元,根据数量=总价÷单价结合如果卖出相同数量的电脑去年销售额为10万元而今年销售额只有8万元,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设该公司可购进m台甲种电脑,则可购进(15-m)台乙种电脑,根据总价=单价×数量结合总价不多于4.8万元且不少于4.7万元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为正整数即可得出各进货方案.
(1)设今年三月份甲种电脑每台售价为x元,则去年同期甲种电脑每台售价为(x+900)元,
依题意,得: ![]() ,
,
解得:x=3600,
经检验,x=3600是所列分式方程的解,且符合题意.
答:今年三月份甲种电脑每台售价为3600元.
(2)设该公司可购进m台甲种电脑,则可购进(15﹣m)台乙种电脑,
依题意,得:![]() ,
,
解得:5≤m≤7![]() .
.
∵m为正整数,
m=5,6,7,
∴该公司共有三种进货方案,方案1:购进5台甲种电脑,10台乙种电脑;方案2:购进6台甲种电脑,9台乙种电脑;方案3:购进7台甲种电脑,8台乙种电脑.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名是从哪个方向看的;(填正面或上面)
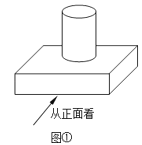
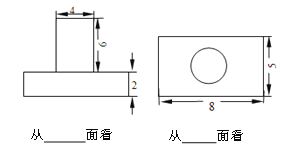
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积和体积.(用含π的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形“.如图为点A,C的“极好菱形”的一个示意图.已知点M的坐标为(1,1),点P的坐标为(3,3).

(1)点E(2,4),F(3,2),G(4,0)中,能够成为点M,P的“极好菱形“的顶点的是 ;
(2)若点M,P的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标;
(3)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;
②当四边形MNPQ的面积为12,且与直线y=x+b有公共点时,请写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AO⊥BO,垂足为点O,直线CD经过点O,下列结论正确的是( )
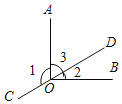
A.∠1+∠2=180°B.∠1﹣∠2=90°C.∠1﹣∠3=∠2D.∠1+∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公交车行驶在笔直的公路上,这条路上有![]() ,
,![]() ,
,![]() ,
,![]() 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在![]() ,
,![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.

(1)问第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
(2)若第一班上行车行驶时间为![]() 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为![]() 千米,求
千米,求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)一乘客前往![]() 站办事,他在
站办事,他在![]() ,
,![]() 两站间的
两站间的![]() 处(不含
处(不含![]() ,
,![]() 站),刚好遇到上行车,
站),刚好遇到上行车,![]() 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到![]() 站或走到
站或走到![]() 站乘下行车前往
站乘下行车前往![]() 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求![]() 满足的条件.
满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校落实新课改精神的情況,现以该校某班的同学参加课外活动的情况为样本,对其参加“球类”“绘画类”“舞蹈类”“音乐类”“棋类”活动的情况进行调査统计,并绘制了如图所示的统计图.
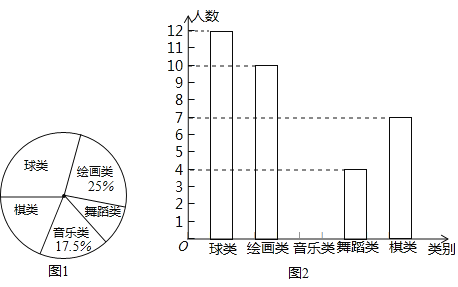
(1)参加音乐类活动的学生人数为 人,参加球类活动的人数的百分比为 ;
(2)请把条形统计图补充完整;
(3)若该校学生共1600人,那么参棋类活动的大约有多少人?
(4)该班参加舞蹈类活动4位同学中,有1位男生(用E表示)和3位女生(分别F,G,H表示),现准备从中选取两名同学组成舞伴,请用列表或画树状的方法求恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们知道,![]() ,类似地,我们把
,类似地,我们把![]() 看成一个整体,则
看成一个整体,则![]()
![]() =
=![]() .“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.
.“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.
尝试应用:
(1)把![]() 看成一个整体,合并
看成一个整体,合并![]() 的结果为_______.
的结果为_______.
(2)已知![]() ,求
,求![]() 的值.
的值.
拓广探索:
(3)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点A和点B分别位于原点O两侧,点A对应的数为a,点B对应的数为b,且|a-b|=7
(1)若b=-3,则a的值为__________;
(2)若OA=3OB,求a的值;
(3)点C为数轴上一点,对应的数为c.若O为AC的中点,OB=3BC,求所有满足条件的c的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com