
【题目】在平面直角坐标系中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形“.如图为点A,C的“极好菱形”的一个示意图.已知点M的坐标为(1,1),点P的坐标为(3,3).

(1)点E(2,4),F(3,2),G(4,0)中,能够成为点M,P的“极好菱形“的顶点的是 ;
(2)若点M,P的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标;
(3)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;
②当四边形MNPQ的面积为12,且与直线y=x+b有公共点时,请写出b的取值范围.
【答案】(1)G;(2)正方形另外两个顶点的坐标为(1,3)、(3,1);(3)①S四边形MNPQ=4;②﹣6≤b≤6.
【解析】
(1)如图1中,观察图象可知:G能够成为点M,P的“极好菱形”顶点.
(2)先求得对角线PM的长,从而可得到正方形的边长,然后可得到这个正方形另外两个顶点的坐标.
(3)①先依据题意画出图形,然后可证明该四边形为正方形,从而可求得它的面积;
②根据菱形的性质得:PM⊥QN,且对角线互相平分,由菱形的面积为12,且菱形的面积等于两条对角线积的一半,可得QN的长,推出Q,N的坐标,再利用一次函数性质解决问题即可.
解:(1)如图1中,由题意点M,P的“极好菱形“的顶点,在线段PM的垂直平分线上.
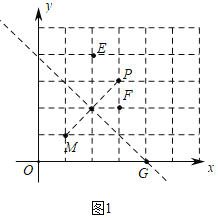
观察图象可知:满足条件的点是点G,
故答案为G.
(2)如图2所示:
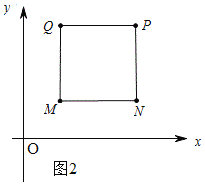
∵点M的坐标为(1,1),点P的坐标为(3,3),
∴MP=2![]() ,
,
∵“极好菱形”为正方形,其对角线长为2![]() ,
,
∴其边长为2.
∴这个正方形另外两个顶点的坐标为(1,3)、(3,1).
(3)①如图2所示:
∵M(1,1),P(3,3),N(3,1),
∴MN=2,PN⊥MN.
∵四边形MNPQ是菱形,
∴四边形MNPQ是正方形.
∴S四边形MNPQ=4..
②如图3所示:
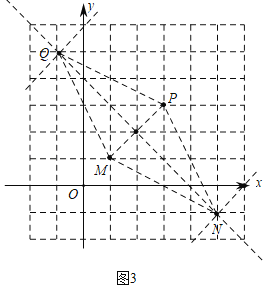
∵点M的坐标为(1,1),点P的坐标为(3,3),
∴PM=2![]() ,
,
∵菱形MNPQ的面积为12,
∴S菱形MNPQ=![]() PMQN=12,即
PMQN=12,即![]() ×2
×2![]() ×QN=12,
×QN=12,
∴QN=6![]() ,
,
∴Q(﹣1,5),N(5,﹣1),
当直线y=x+b经过点Q(﹣1,5)时,b=6,
当y=x+b经过点N(5,﹣1)时,b=﹣6,
∴当四边形MNPQ与直线y=x+b有公共点时,b的取值范围是﹣6≤b≤6.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】某家具厂生产一种课桌和椅子,课桌每张定价200 元,椅子每把定价80元,厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:每买一张课桌就赠送一把椅子;方案二:课桌和椅子都按定价的80%付款.某校计划添置100张课桌和x把椅子.
(1)若x>100,请用含x的代数式分别把两种方案的费用表示出来;
(2)若x=300,如果两种方案可以同时使用,作为一种新的方案,请帮助学校设计一种最省钱的方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形桌子可坐6人,按图3将桌子拼在一起.

(1)2张桌子拼在一起可坐 人,4张桌子拼在一起可坐 人,n张桌子拼在一起可坐 人;
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为1∶2的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使![]() ,连接EC并延长,使
,连接EC并延长,使![]() ,连接
,连接![]() 为FG的中点,连接DH.
为FG的中点,连接DH.
![]() 求证:四边形AFHD为平行四边形;
求证:四边形AFHD为平行四边形;
![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(x-1)(x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
(x-1)(x4+x3+x2+x+1)= ,
………
猜想:(x-1)(xn+xn-1+…+x2+x+1)= ,
(2)根据以上结果,试写出下面两式的结果
①(x-1)(x49+x48+…+x2+x+1)= ,
②(x20-1)÷(x-1)= ,
(3)利用以上结论求值:1+3+32+33+34+……+32018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,受各方因素影响,电脑价格将不断下降,今年三月份的电脑售价比去年同期每台降价900元,如果卖出相同数量的电脑,去年销售为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3400元,乙种电脑每台进价为3000元,公司预计用不多于4.8万元且不少于4.7万元的资金购进这两种电脑共15台,则共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的全体同学排成一列步行去市博物馆参加科技活动,小涛担任通讯员.在队伍中,小涛先数了一下他前后的人数,发现前面的人数是后面人数的2倍,他往前超了8名同学后,发现前面的人数和后面的人数一样.
(1)七年级(1)班有多少名同学?
(2)这些同学要过一座长60米的大桥,安全起见,相邻两个同学间保持相同的固定距离,队伍前进速度为1.2米/秒,从第一名同学刚上桥到全体通过大桥用了90秒,则队伍的全长为多少米?
(3)在(2)的条件下,排在队尾的小刚想把一则通知送到队伍最前的小婷手中,若小刚从队尾追赶小婷的速度是4.2米/秒,他能在15秒内追上小婷吗?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com