
【题目】小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为1∶2的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.

科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为 1,A、B、C 都在格点上(小正方形的顶点叫做格点).请仅用没有刻度的直尺完成画图(不要求写画法)及解答:
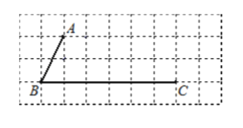
(1)过点C画直线AB的平行线CD;
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H;
(3)线段 的长度是点 A 到直线 BC 的距离;
(4)∠B与∠HAG的大小关系为 ,理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过点A作AE//BC与过点D作CD的垂线交于点E.
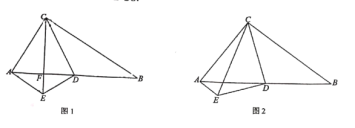
(1)如图1,若CE交AD于点F,BC=6,∠B=30°,求AE的长
(2)如图2,求证AE+CE=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠B=90°,AB=5![]() ,点E在AB上,∠AED=45°,DE=6,CE=7.求AE的长及sin∠BCE的值.
,点E在AB上,∠AED=45°,DE=6,CE=7.求AE的长及sin∠BCE的值.
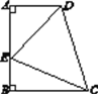
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形“.如图为点A,C的“极好菱形”的一个示意图.已知点M的坐标为(1,1),点P的坐标为(3,3).

(1)点E(2,4),F(3,2),G(4,0)中,能够成为点M,P的“极好菱形“的顶点的是 ;
(2)若点M,P的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标;
(3)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;
②当四边形MNPQ的面积为12,且与直线y=x+b有公共点时,请写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
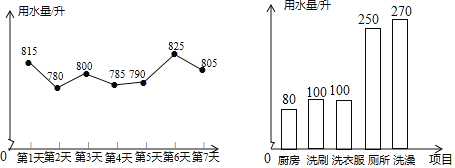
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)若规定居民生活用水收费标准为2.80元/立方米,请你估算小申家一个月(按30天计算)的水费是多少元?(1立方米=1000升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公交车行驶在笔直的公路上,这条路上有![]() ,
,![]() ,
,![]() ,
,![]() 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在![]() ,
,![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.

(1)问第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
(2)若第一班上行车行驶时间为![]() 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为![]() 千米,求
千米,求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)一乘客前往![]() 站办事,他在
站办事,他在![]() ,
,![]() 两站间的
两站间的![]() 处(不含
处(不含![]() ,
,![]() 站),刚好遇到上行车,
站),刚好遇到上行车,![]() 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到![]() 站或走到
站或走到![]() 站乘下行车前往
站乘下行车前往![]() 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求![]() 满足的条件.
满足的条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com