
科目:初中数学 来源: 题型:
 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 购买商品A的数量 | 购买商品B的数量 | 购买总费用(元) | |
| 第一次购物 | 1 | 2 | 330 |
| 第二次购物 | 6 | 7 | 1380 |
| 第三次购物 | 9 | 8 | 1062 |
查看答案和解析>>
科目:初中数学 来源: 题型:
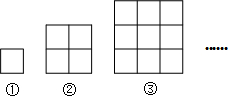 如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )
如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )| A、55 | B、78 | C、91 | D、140 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com